算法训练3.2.2 背包模型

前言

背包模型的核心在于：n 个物品做一些选择，使得最终 值最大/值最小/数量最多等。解题思路就是：挨个物品考虑，每个物品有两种选择：选和不选。

背包最常见的两类模型：

  • 01背包：f(i, j) → f(i - 1, j), f(i - 1, j - v[i])。f(i, j) 只依赖于 f(i - 1, j) 和 f(i - 1, j - v[i])。因此base case是 f(0, j)，一般 dp 数组定义为 dp[n + 1][w + 1]，这样 dp[0][j] 的含义就是没有物品的时候的最优解，这样做是为了 便于初始化。
  • 完全背包：f(i, j) → f(i - 1, j), f(i, j - v[i])。f(i, j) 只依赖于 f(i - 1, j) 和 f(i, j - v[i])。可以看出，“完全背包”和“01背包”的区别只在于 选的时候 依赖不同，因为物品是不限制数量的，因此就算选了第 i 个物品，也可以继续考虑第 i 个物品。

代码模板如下：

01背包模板

1
2
3
4
5
6
7
8
9
10
11
int n, C; //n个物品， C表示背包容量
int[] v,  w; //v[i]表示第i个物品的价格/体积    w[i]表示第i个物品的价值
int[][] dp = new int[n + 1][C + 1]; //容器规模
dp[0][j]; //初始化
for (int i = 1 ; i <= n ; i++) {
    for (int j = 0 ; j <= C ; j++) {
        if (j >= v[i - 1]) dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i-1]] + w[i - 1]);
        else dp[i][j] = dp[i - 1][j];
    }
}
return dp[n][C];

完全背包模板

1
2
3
4
5
6
7
8
9
10
11
int n, C; //n个物品， C表示背包容量
int[] v,  w; //v[i]表示第i个物品的价格/体积    w[i]表示第i个物品的价值
int[][] dp = new int[n + 1][C + 1]; //容器规模
dp[0][j]; //初始化
for (int i = 1 ; i <= n ; i++) {
    for (int j = 0 ; j <= C ; j++) {
        if (j >= v[i - 1]) dp[i][j] = max(dp[i-1][j], dp[i][j-v[i-1]] + w[i - 1]);
        else dp[i][j] = dp[i - 1][j];
    }
}
return dp[n][C];

滚动数组：不难发现“01背包”和“完全背包”的依赖关系都取决于 (i - 1, j - a) 和 (i, j - a)。因此可以用一个 一维数组 dp[j] 来表示这个过程，也就是初始化的时候 dp[j] 表示的是 i == 0 的值，然后依次将 dp[j] 改为 1, 2, 3, …., n的值。

01背包 的依赖如下：

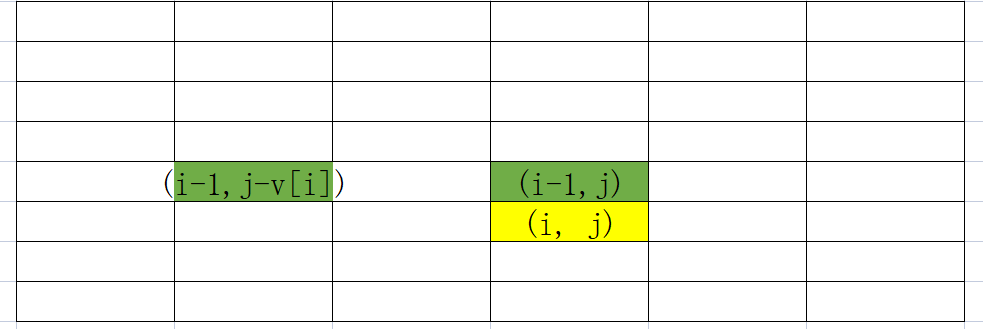
01背包依赖关系

对于任意节点（黄色）(i, j) 都依赖于上一行的两个值也就是 i - 1 这一行的值。因此可以 复用一个一维数组 来替代二维数组。注意：01背包使用一维数组表示一定要从一维数组从大到小来进行填表，否则会导致依赖的值被覆盖而导致出错！

01背包一维表示

1
2
3
4
5
6
7
8
9
10
int n, C; //n个物品， C表示背包容量
int[] v,  w; //v[i]表示第i个物品的价格/体积    w[i]表示第i个物品的价值
int[] dp = new int[C + 1]; //容器规模
dp[j]; //初始化
for (int i = 1 ; i <= n ; i++) {
    for (int j = C ; j >=  v[i - 1] ; j--) {
        dp[j] = max(dp[j], dp[j-v[i-1]] + w[i - 1]);
    }
}
return dp[C];

完全背包的依赖如下：

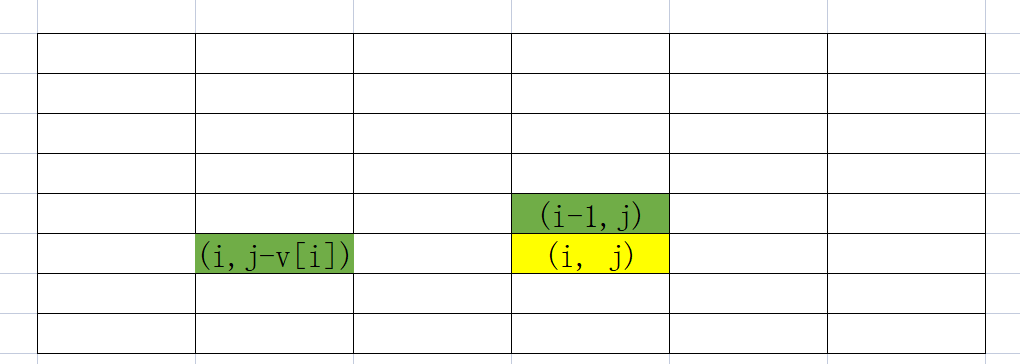
完全背包依赖关系

对于任意节点（黄色）(i, j) 都依赖于 (i - 1,j) 和 (i, j - v[i])。因此依然可以 复用一个一维数组 来替代二维数组。注意：完全背包使用一维数组表示一定要从一维数组从小到大来进行填表，否则会出现依赖的值还没算而依赖错值！

1
2
3
4
5
6
7
8
9
10
int n, C; //n个物品， C表示背包容量
int[] v,  w; //v[i]表示第i个物品的价格/体积    w[i]表示第i个物品的价值
int[] dp = new int[C + 1]; //容器规模
dp[j]; //初始化
for (int i = 1 ; i <= n ; i++) {
    for (int j = v[i - 1] ; j <= c ; j++) {
        dp[j] = max(dp[j], dp[j-v[i-1]] + w[i - 1]);
    }
}
return dp[C];

分割等和子集

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

提示：

1 <= nums.length <= 200
1 <= nums[i] <= 100

题目解析

“一个数组是否可以平均分为2份”等价于“能否找到一个子集，使得子集的和为数组总和的一半”。

因此，这就是一个01背包问题。数组中的数字就是物品，总和一半就是背包容量。

因此可以直接条用背包的模板。

  • 状态转移方程式：dp[i][j] 表示考虑前 i 个数字，能否凑出 j。第 i 个数字可以选也可以不选，也就是 dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]]
  • 容器规模：i 表示数字，范围为 [0, n]。j 表示背包容量，范围为 [0, target]
  • base case：dp[0][j]，含义是考虑第 0 个数字（也就是没有数字）的时候，能否凑出 j，因此只能凑出0，所以 dp[0][0] = true，其他的均为 false。
  • 填表顺序：从 i=1 行开始填，一行一行填即可。

代码展示

二维背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    // canPartition方法用于判断一个整数数组nums是否可以被分割成两个和相等的子集
    public boolean canPartition(int[] nums) {
        // 计算数组nums中所有元素的和
        int sum = 0;
        for (int num : nums) sum += num;
        
        // 如果总和是奇数，则无法分割成两个相等的子集，直接返回false
        if (sum % 2 != 0) return false;
        
        // 数组长度和需要达到的和（总和的一半）
        int n = nums.length;
        int target = sum / 2;
        
        // 创建一个二维数组dp，用于存储动态规划过程中的状态
        // dp[i][j]表示在考虑了前i个数字的情况下，是否能够找到和为j的子集
        boolean[][] dp = new boolean[n + 1][target + 1];
        
        // 初始化dp数组的第一行，当不选择任何数字时，无法形成任何和，即所有dp[0][j]都是false
        // 除了dp[0][0]表示和为0是始终可达到的，因此设为true
        dp[0][0] = true;
        
        // 外层循环遍历数组nums
        for (int i = 1 ; i <= n ; i++) {
            // 内层循环遍历和的范围，从0到target
            for (int j = 0 ; j <= target ; j++) {
                // 如果当前考虑的数字可以满足当前的和j（即j大于等于nums[i-1]）
                // 则有两种情况可以达到和j：不选择当前数字，或选择当前数字
                // 不选择当前数字的情况：dp[i-1][j]，选择当前数字的情况：dp[i-1][j-nums[i-1]]
                if (j >= nums[i - 1]) dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];
                // 如果当前考虑的数字不能满足当前的和j，则只能考虑不选择当前数字的情况
                else dp[i][j] = dp[i - 1][j];
            }
        }
        
        // 返回dp[n][target]，即考虑了所有数字后，是否能够找到和为目标值target的子集
        return dp[n][target];
    }
}

一维背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    // canPartition方法用于判断一个整数数组nums是否可以被分割成两个和相等的子集
    public boolean canPartition(int[] nums) {
        // 计算数组nums中所有元素的和
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        // 如果总和是奇数，则无法分割成两个相等的子集，直接返回false
        if (sum % 2 != 0) {
            return false;
        }
        // 数组长度和需要达到的和（总和的一半）
        int n = nums.length;
        int target = sum / 2;
        // 创建一个一维数组dp，用于存储动态规划过程中的状态
        // dp[j]表示在考虑了前i个数字的情况下，是否能够找到和为j的子集
        boolean[] dp = new boolean[target + 1];
        // 初始化dp数组，dp[0]为true，因为和为0始终可达到
        dp[0] = true;
        // 外层循环遍历数组nums
        for (int i = 1; i <= n; i++) {
            // 内层循环从target往回遍历到nums[i-1]
            // 因为如果dp[j]在遍历到j-nums[i-1]时已经为true，则不需要再次检查
            for (int j = target; j >= nums[i - 1]; j--) {
                // dp[j]表示在前i-1个数字中能否找到和为j的子集
                // 则在考虑第i个数字后，有两种情况可以达到和为j：
                // 1. 不选择第i个数字，即保持dp[j]不变
                // 2. 选择第i个数字，即dp[j] = dp[j - nums[i - 1]]
                // 因此，更新dp[j] = dp[j] || dp[j - nums[i - 1]]
                dp[j] = dp[j] || dp[j - nums[i - 1]];
            }
        }
        // 返回dp[target]，即考虑了所有数字后，是否能够找到和为目标值target的子集
        return dp[target];
    }
}

目标和

给你一个整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 “+2-1” 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例 1：

输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：

输入：nums = [1], target = 1
输出：1

提示：

1 <= nums.length <= 20

0 <= nums[i] <= 1000

0 <= sum(nums[i]) <= 1000

-1000 <= target <= 1000

题目描述

假设数组总和为 sum，添加 - 号的元素的和为 neg，则其余添加 + 号的元素之和为 sum - neg，则我们要求的最终表达式是 + 号的元素减去 - 号的元素的值为 target，也就是：

(sum−neg)−neg=sum−2⋅neg=target(sum−neg)−neg=sum−2⋅neg=target

将式子展开：

neg=(sum−target)÷2neg=(sum−target)÷2

因此，问题转换成 在数组中能找到多少个和为 neg 的子集。

这就是 01背包 问题。

  • 状态转移方程式：dp[i][j] 表示考虑前 i 个数字，能凑出多少个和为 j 的子集。第 i 个数字可以选也可以不选，也就是 dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]]
  • 容器规模：i 表示数字，范围为 [0, n]。j 表示背包容量，范围为 [0, neg]
  • base case：dp[0][j]，含义是考虑第 0 个数字（也就是没有数字）的时候，能凑出多少个和为 j 的子集，因此只能凑出 0，所以 dp[0][0] = 1，其他的均为 0。
  • 填表顺序：从 i=1 行开始填，一行一行填即可。

代码展示

二维背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
    // findTargetSumWays方法用于计算给定数组nums和目标和target时，有多少种不同的组合方式
    // 使得组合中的数字和为目标target
    public int findTargetSumWays(int[] nums, int target) {
        // 计算数组nums中所有元素的和
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        // 如果总和与目标和target之差为奇数，则无法通过加减得到目标和，直接返回0
        if ((sum - target) % 2 != 0) {
            return 0;
        }
        // 计算需要达到目标和需要减去的数值（总和与目标和之差的一半）
        int neg = (sum - target) / 2;
        // 如果需要减去的数值为负数，则无法通过加减得到目标和，直接返回0
        if (neg < 0) {
            return 0;
        }
        // 创建一个二维数组dp，用于存储动态规划过程中的状态
        // dp[i][j]表示在考虑了前i个数字的情况下，有多少种方法使得这些数字的和为j
        int[][] dp = new int[nums.length + 1][neg + 1];
        // 初始化dp数组，当不选择任何数字时，只有一种方法使得和为0，即dp[0][0]为1
        dp[0][0] = 1;
        // 外层循环遍历数组nums
        for (int i = 1; i <= nums.length; i++) {
            // 内层循环遍历需要达到的和的范围，从0到neg
            for (int j = 0; j <= neg; j++) {
                // 如果当前考虑的数字可以满足当前的和j（即j大于等于nums[i-1]）
                // 则有两种情况可以达到和为j：
                // 1. 不选择当前数字，即保持dp[i-1][j]不变
                // 2. 选择当前数字，即dp[i-1][j - nums[i - 1]]
                // 因此，更新dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i - 1]]
                if (j >= nums[i - 1]) {
                    dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i - 1]];
                } else {
                    // 如果当前考虑的数字不能满足当前的和j，则只能考虑不选择当前数字的情况
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        // 返回dp[nums.length][neg]，即考虑了所有数字后，有多少种方法使得这些数字的和为目标和的一半
        return dp[nums.length][neg];
    }
}

一维背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    // findTargetSumWays方法用于计算给定数组nums和目标和target时，
    // 有多少种不同的组合方式使得组合中的数字和加上负号的数字和为目标target
    public int findTargetSumWays(int[] nums, int target) {
        // 计算数组nums中所有元素的和
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        // 如果总和与目标和target之差为奇数，则无法通过加减得到目标和，直接返回0
        if ((sum - target) % 2 != 0) {
            return 0;
        }
        // 计算需要达到目标和需要减去的数值（总和与目标和之差的一半）
        int neg = (sum - target) / 2;
        // 如果需要减去的数值为负数，则无法通过加减得到目标和，直接返回0
        if (neg < 0) {
            return 0;
        }
        // 创建一个一维数组dp，用于存储动态规划过程中的状态
        // dp[j]表示在考虑了前i个数字的情况下，有多少种方法使得这些数字的和为j
        int[] dp = new int[neg + 1];
        // 初始化dp数组，当不选择任何数字时，只有一种方法使得和为0，即dp[0]为1
        dp[0] = 1;
        // 外层循环遍历数组nums
        for (int i = 1; i <= nums.length; i++) {
            // 内层循环从neg往回遍历到nums[i-1]的绝对值
            // 因为如果dp[j]在遍历到j-nums[i-1]时已经确定，则不需要再次检查
            for (int j = neg; j >= nums[i - 1]; j--) {
                // dp[j]表示在前i-1个数字中有多少种方法使得和为j
                // 则在考虑第i个数字后，有两种情况可以达到和为j：
                // 1. 不选择第i个数字，即保持dp[j]不变
                // 2. 选择第i个数字，并减去其值，即dp[j] += dp[j - nums[i - 1]]
                // 因此，更新dp[j] = dp[j] + dp[j - nums[i - 1]]
                dp[j] = dp[j] + dp[j - nums[i - 1]];
            }
        }
        // 返回dp[neg]，即考虑了所有数字后，有多少种方法使得这些数字的和加上负号的数字和为目标target
        return dp[neg];
    }
}

其他解法

这个 01背包 的转换可能并不是特别好想，也可以使用直观的 dp 进行表示，也就是加+号和加-号的情况。

dp[i][j] = dp[i -1][j + nums[i]] + dp[i - 1][j - nums[i]]

但是这种做法并不好做，因为 j 是会出现负数的情况的，因此我们需要进行处理，因为sum(nums)最大是1000，那全部加-号就是 -1000，因此我们可以整体加1000进行处理，将负数转成正数。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    // findTargetSumWays方法用于计算给定数组nums和目标和target时，
    // 有多少种不同的组合方式使得组合中的数字和为目标target
    public int findTargetSumWays(int[] nums, int target) {
        // 计算数组nums中所有元素的和
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }

        // 创建一个二维数组dp，用于存储动态规划过程中的状态
        // dp[i][j]表示在考虑了前i个数字的情况下，有多少种方法使得这些数字的和为j
        // 由于sum可能很大，为了避免索引越界，我们使用1000作为偏移量
        int[][] dp = new int[nums.length + 1][2010];

        // 初始化dp数组，当不选择任何数字时，只有一种方法使得和为0
        // 因此，dp[0][0 + 1000]设为1，其中1000是偏移量
        dp[0][0 + 1000] = 1;

        // 外层循环遍历数组nums，从1开始，表示从数组的第一个元素开始考虑
        for (int i = 1; i <= nums.length; i++) {
            // 内层循环遍历所有可能的和，从-sum到sum
            // 由于我们使用了偏移量，所以实际索引范围是[0, 2010]
            for (int j = -sum; j <= sum; j++) {
                // 如果考虑当前数字nums[i - 1]后，新的和j-nums[i - 1]在有效范围内
                // 则从dp[i - 1][j - nums[i - 1] + 1000]的状态转移而来
                if (j - nums[i - 1] >= -sum) {
                    dp[i][j + 1000] += dp[i - 1][j - nums[i - 1] + 1000];
                }
                // 如果考虑当前数字nums[i - 1]后，新的和j+nums[i - 1]在有效范围内
                // 则从dp[i - 1][j + nums[i - 1] + 1000]的状态转移而来
                if (j + nums[i - 1] <= sum) {
                    dp[i][j + 1000] += dp[i - 1][j + nums[i - 1] + 1000];
                }
            }
        }

        // 返回dp[nums.length][target + 1000]，即考虑了所有数字后，
        // 有多少种方法使得这些数字的和为目标和target
        return dp[nums.length][target + 1000];
    }
}

一和零

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1：

输入：strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ，因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：

输入：strs = [“10”, “0”, “1”], m = 1, n = 1
输出：2
解释：最大的子集是 {“0”, “1”} ，所以答案是 2 。

提示：

1 <= strs.length <= 600
1 <= strs[i].length <= 100
strs[i] 仅由 ‘0’ 和 ‘1’ 组成
1 <= m, n <= 100

题目解析

此题是裸背包问题，不需要进行转换，不同的是背包的限制有两个维度，一个是 0 的数量，一个 1 的数量。

  • 状态转移方程式：dp[i][j][k] 表示考虑前 i 个字符串，有 j 个 0 和 k 个 1，可以选取的最大子集是多大。 dp[i][j][k] = max(dp[i-1][j][k] , dp[i-1][j - zeros[i]][k - ones[i]] + 1)，zeros[i] 表示第 i 个字符串有多少个0，ones[i] 表示第 i 个字符串有多少个 1。
  • 容器规模：i 表示第几个字符串，范围是 [0, length]。j 表示剩余的 0 的数量，范围是 [0, m]。k 表示剩余 1 的数量，范围是 [0, n]
  • base case：dp[0][j][k] 考虑第 0 个字符（没有字符）的时候，可以凑出的最大子集，那就都是 0 就好了。
  • 填表顺序：i 从 1 开始填到 n 即可。

代码展示

三维背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
    // findMaxForm方法用于找出给定字符串数组strs，可以形成多少个大小为m*n的矩阵
    // 其中'0'的数量不超过m，'1'的数量不超过n
    public int findMaxForm(String[] strs, int m, int n) {
        int len = strs.length; // 获取字符串数组的长度
        // 初始化两个数组，用于存储每个字符串中'1'和'0'的数量
        int[] ones = new int[len];
        int[] zeros = new int[len];
        // 遍历字符串数组，分别计算每个字符串中'1'和'0'的数量
        for (int i = 0; i < len; i++) {
            ones[i] = count(strs[i], '1');
            zeros[i] = count(strs[i], '0');
        }
        // 初始化三维动态规划数组dp，用于存储状态
        // dp[i][j][k]表示考虑前i个字符串，使用j个'0'和k个'1'时，可以形成矩阵的最大数量
        int[][][] dp = new int[strs.length + 1][m + 1][n + 1];

        // 外层循环遍历字符串数组strs
        for (int i = 1; i <= strs.length; i++) {
            // 中层循环遍历'0'的使用数量，不超过m
            for (int j = 0; j <= m; j++) {
                // 内层循环遍历'1'的使用数量，不超过n
                for (int k = 0; k <= n; k++) {
                    // 如果当前考虑的字符串中的'0'数量不超过j，'1'数量不超过k
                    // 则可以从dp[i-1][j-zeros[i - 1]][k-ones[i - 1]]转移而来，并加1
                    if (j - zeros[i - 1] >= 0 && k - ones[i - 1] >= 0) {
                        dp[i][j][k] = Math.max(
                            // 选择当前字符串，更新j和k
                            dp[i - 1][j - zeros[i - 1]][k - ones[i - 1]] + 1,
                            // 不选择当前字符串，保持j和k不变
                            dp[i - 1][j][k]
                        );
                    } else {
                        // 如果不满足条件，则只能从dp[i-1][j][k]转移而来
                        dp[i][j][k] = dp[i - 1][j][k];
                    }
                }
            }
        }
        // 返回dp[strs.length][m][n]，即考虑所有字符串后，可以形成的最大矩阵数量
        return dp[len][m][n];
    }

    // count方法用于计算字符串str中有多少个target字符
    public int count(String str, Character target) {
        int count = 0; // 初始化计数器
        // 遍历字符串str中的每个字符
        for (char c : str.toCharArray()) {
            // 如果当前字符等于target，则计数器加1
            if (c == target) {
                count++;
            }
        }
        return count; // 返回计数结果
    }
}

二维背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class Solution {
    // findMaxForm方法用于找出给定字符串数组strs，可以形成多少个大小为m*n的矩阵
    // 其中'0'的数量不超过m，'1'的数量不超过n
    public int findMaxForm(String[] strs, int m, int n) {
        int len = strs.length; // 获取字符串数组的长度
        // 初始化两个数组，用于存储考虑每个字符串后，'1'和'0'的最大数量
        int[] ones = new int[len + 1];
        int[] zeros = new int[len + 1];
        
        // 计算每个字符串中'1'和'0'的数量，并更新ones和zeros数组
        for (int i = 1; i <= len; i++) {
            ones[i] = count(strs[i - 1], '1');
            zeros[i] = count(strs[i - 1], '0');
        }
        
        // 初始化二维动态规划数组dp，用于存储状态
        // dp[j][k]表示使用'0'的数量不超过j，'1'的数量不超过k时最大子集的长度
        int[][] dp = new int[m + 1][n + 1];
        
        // 外层循环遍历字符串数组strs
        for (int i = 1; i <= strs.length; i++) {
            // 由于我们需要从后向前更新dp数组以避免重复计算，因此两层内层循环从m和n开始递减
            for (int j = m; j >= zeros[i]; j--) {
                for (int k = n; k >= ones[i]; k--) {
                    // 更新dp数组，选择包含当前字符串或不包含当前字符串的较大值
                    dp[j][k] = Math.max(
                        // 选择当前字符串，更新j和k表示的'1'和'0'的数量
                        dp[j - zeros[i]][k - ones[i]] + 1,
                        // 不选择当前字符串，保持j和k不变
                        dp[j][k]
                    );
                }
            }
        }
        // 返回dp[m][n]，即在'0'的数量不超过m，'1'的数量不超过n时最大子集的长度
        return dp[m][n];
    }

    // count方法用于计算字符串str中有多少个target字符
    public int count(String str, Character target) {
        int count = 0; // 初始化计数器
        // 遍历字符串str中的每个字符
        for (char c : str.toCharArray()) {
            // 如果当前字符等于target，则计数器加1
            if (c == target) {
                count++;
            }
        }
        // 返回计数结果
        return count;
    }
}

零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

输入：coins = [1, 2, 5], amount = 11
输出：3
解释：11 = 5 + 5 + 1

示例 2：

输入：coins = [2], amount = 3
输出：-1

示例 3：

输入：coins = [1], amount = 0
输出：0

提示：

1 <= coins.length <= 12

1 <= coins[i] <= 2^31 - 1

0 <= amount <= 10^4

题目解析

此题是典型的完全背包问题。

  • 状态转移方程式：dp[i][j] 考虑前 i 个硬币，凑出 j 元最少需要的硬币数。dp[i][j] = min(dp[i - 1][j], dp[i][j - coins[i])
  • 容器规模：i 的范围是 [0, coins.length]，j 的范围是 [0, amount]
  • base case：dp[0][j] 表示考虑前 0 个硬币凑出 j 的最少硬币数，除了 dp[0][0] = 0 以外，其余的均凑不了，也就是没有硬币的情况下，只能凑出 0，其他的金额都凑不了，因此这里用一个比较大的数字表示（因为 amount 最大是10^4，因此我们用10001表示最大值）
  • 顺序：i = 1 开始填表。

代码展示

二维背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    // coinChange方法用于计算达到指定金额amount最少需要多少个硬币
    // coins数组表示可用的硬币面额
    public int coinChange(int[] coins, int amount) {
        // dp[i][j]表示使用coins前i种硬币组成金额j时的最少硬币数量
        int[][] dp = new int[coins.length + 1][amount + 1];
        
        // 初始化dp数组的第一行，将所有值设为一个较大的数（不可能的硬币数量）
        // 除了dp[0][0]，表示组成金额0时不需要任何硬币
        Arrays.fill(dp[0], 10001);
        dp[0][0] = 0;
        
        // 外层循环遍历硬币面额数组coins
        for (int i = 1; i <= coins.length; i++) {
            // 内层循环遍历金额从0到amount
            for (int j = 0; j <= amount; j++) {
                // 如果当前金额j大于等于硬币面额coins[i-1]
                // 则考虑使用该硬币，更新dp[i][j]
                // dp[i][j]取dp[i-1][j]（不使用当前硬币）和dp[i][j-coins[i-1]] + 1（使用当前硬币）的较小值
                if (j >= coins[i - 1]) {
                    dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - coins[i - 1]] + 1);
                } else {
                    // 如果当前金额j小于硬币面额coins[i-1]，则不能使用这个硬币
                    // 更新dp[i][j]为dp[i-1][j]，即继承之前的状态
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        
        // 如果dp[coins.length][amount]仍然为初始化的10001，表示无法组成金额amount
        // 返回-1表示无解
        // 否则返回dp[coins.length][amount]，即组成金额amount的最少硬币数量
        return dp[coins.length][amount] == 10001 ? -1 : dp[coins.length][amount];
    }
}

一维背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    // coinChange方法用于计算达到指定金额amount最少需要多少个硬币
    // coins数组表示可用的硬币面额
    public int coinChange(int[] coins, int amount) {
        // 创建一个一维动态规划数组dp，用于存储状态
        // dp[j]表示组成金额j时的最少硬币数量
        int[] dp = new int[amount + 1];
        
        // 初始化dp数组，将所有值设为一个较大的数（不可能的硬币数量），除了dp[0]设为0
        // 表示组成金额0时不需要任何硬币
        Arrays.fill(dp, 10001);
        dp[0] = 0;
        
        // 外层循环遍历硬币面额数组coins
        for (int i = 1; i <= coins.length; i++) {
		        // 完全背包，从小到大填
            // 内层循环从当前硬币面额开始，遍历到金额amount
            for (int j = coins[i - 1]; j <= amount; j++) {
                // 对于每个金额j，尝试使用当前硬币面额coins[i-1]
                // 更新dp[j]为不使用当前硬币的dp[j]与使用当前硬币的dp[j - coins[i - 1]] + 1中的较小值
                dp[j] = Math.min(dp[j], dp[j - coins[i - 1]] + 1);
            }
        }
        
        // 最后检查dp[amount]，如果仍然为初始化的10001，表示无法组成金额amount
        // 返回-1表示无解
        // 否则返回dp[amount]，即组成金额amount的最少硬币数量
        return dp[amount] == 10001 ? -1 : dp[amount];
    }
}

零钱兑换 II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

示例 1：

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2：

输入：amount = 3, coins = [2]
输出：0
解释：只用面额 2 的硬币不能凑成总金额 3 。

示例 3：

输入：amount = 10, coins = [10]
输出：1

提示：

1 <= coins.length <= 300
1 <= coins[i] <= 5000
coins 中的所有值 互不相同
0 <= amount <= 5000

题目解析

此题是典型的完全背包问题。

  • 状态转移方程式：dp[i][j] 考虑前 i 个硬币，凑出 j 元有多少种方式。dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]
  • 容器规模：i 的范围是 [0, coins.length]，j 的范围是 [0, amount]
  • base case：dp[0][j] 表示考虑前 0 个硬币凑出 j 的有多少种方式，除了 dp[0][0] = 1 以外，其余的均凑不了，也就是没有硬币的情况下，只能凑出 0，其他的金额都凑不了，因此 dp[0][j] = 0， j∈[1, amount]
  • 顺序：i = 1 开始填表。

代码展示

二维背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    // change方法用于计算组成特定金额amount的所有可能的硬币组合数量
    // coins数组表示可用的硬币面额
    public int change(int amount, int[] coins) {
        // dp[i][j]表示使用前i种硬币组成金额j时的硬币组合数量
        int[][] dp = new int[coins.length + 1][amount + 1];
        
        // 初始化dp数组，dp[0][0]为1，表示有1种方式组合金额为0（不使用任何硬币）
        dp[0][0] = 1;
        
        // 外层循环遍历硬币数组coins
        for (int i = 1; i <= coins.length; i++) {
            // 内层循环遍历金额从0到amount
            for (int j = 0; j <= amount; j++) {
                // 如果当前金额j大于等于硬币面额coins[i-1]
                // 则可以有两种选择：使用或不使用当前硬币
                if (j >= coins[i - 1]) {
                    // dp[i][j]更新为不使用当前硬币的组合数量（dp[i - 1][j]）
                    // 加上使用当前硬币的组合数量（dp[i][j - coins[i - 1]]）
                    dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]];
                } else {
                    // 如果当前金额j小于硬币面额coins[i-1]，则不能使用这个硬币
                    // dp[i][j]继承不使用当前硬币的组合数量（dp[i - 1][j]）
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        
        // 返回dp[coins.length][amount]，即使用所有硬币组成金额amount的硬币组合数量
        return dp[coins.length][amount];
    }
}

一维背包

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    // change方法用于计算组成特定金额amount的所有可能的硬币组合数量
    // amount是需要找零的总金额
    // coins是可用的硬币面额数组
    public int change(int amount, int[] coins) {
        // 创建一个一维动态规划数组dp，用于存储组成每个金额的硬币组合数量
        // dp[j]表示组成金额j时的硬币组合数量
        int[] dp = new int[amount + 1];
        // 初始化dp数组，dp[0]为1，表示金额为0时有一种组合方式（不使用任何硬币）
        dp[0] = 1;
        
        // 外层循环遍历硬币数组coins
        for (int i = 1; i <= coins.length; i++) {
            // 内层循环从当前硬币面额开始，到总金额amount结束
            for (int j = coins[i - 1]; j <= amount; j++) {
                // 对于每个金额j，如果当前硬币coins[i - 1]可以用，则更新dp[j]
                // dp[j]表示金额为j的硬币组合数量，更新为不使用当前硬币的组合数量（dp[j]）
                // 和使用当前硬币的组合数量（dp[j - coins[i - 1]])之和
                dp[j] = dp[j] + dp[j - coins[i - 1]];
            }
        }
        
        // 返回dp[amount]，表示组成总金额amount的所有可能的硬币组合数量
        return dp[amount];
    }
}
计算机基础 > 算法
#算法
算法训练3.2.2 背包模型
https://fulequn.github.io/2024/05/Article202405221/
作者
Fulequn
发布于
2024年5月22日
许可协议