算法训练3.1 单调栈自顶向下的动态规划（记忆化搜索）第二部分

零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

输入：coins = [1, 2, 5], amount = 11
输出：3
解释：11 = 5 + 5 + 1

示例 2：

输入：coins = [2], amount = 3
输出：-1

示例 3：

输入：coins = [1], amount = 0
输出：0

提示：
1 <= coins.length <= 12
1 <= coins[i] <= 2^31 - 1
0 <= amount <= 10^4

题目解析

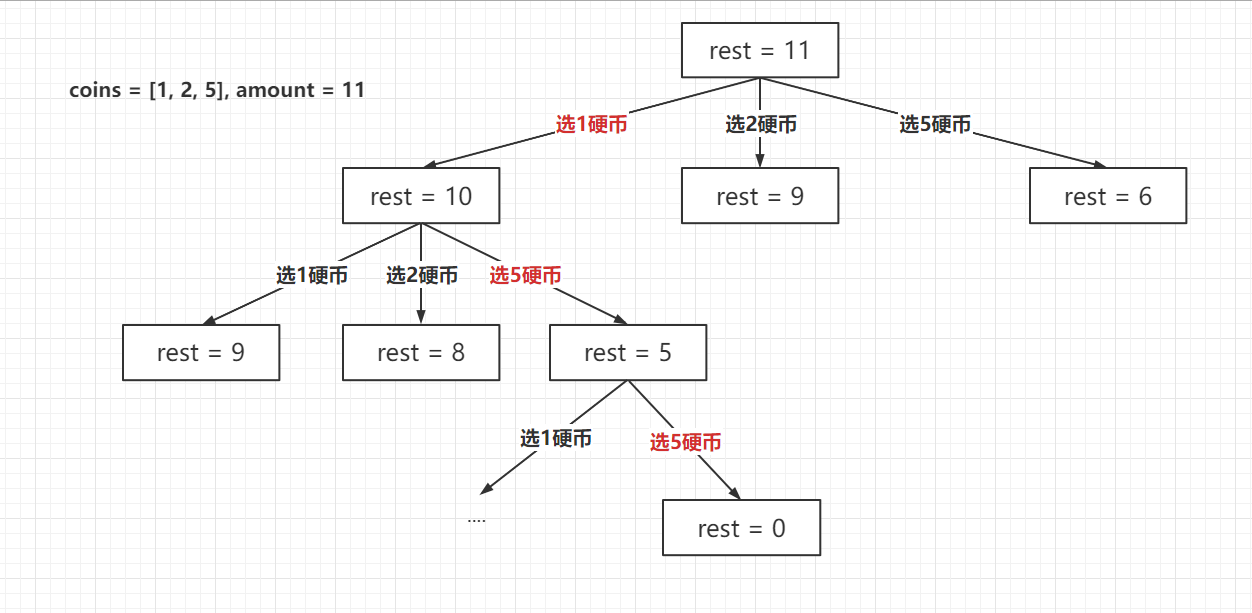
递归的思路如下：以样例1为例，amount=11，要凑11块钱，我们有几种做法，选1，2，5，那我们只需要查询凑出10，9，6分别需要的最少硬币数量即可。

题目解析

递归的三个核心如下：

  • 参数：rest当前需要拼凑的钱数
  • 出口：rest == 0
  • 方向：选择coins中的任意一个硬币，只要不比rest大

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {

    // coinChange 方法用于计算凑齐一定金额所需的最少硬币数量
    // coins 是可用的硬币面额数组，amount 是需要凑齐的金额
    public int coinChange(int[] coins, int amount) {
        // 初始化备忘录数组 mem，大小为 amount + 1，用于存储已经计算过的金额状态
        mem = new int[amount + 1];
        // 使用 Arrays.fill 方法将备忘录数组 mem 填入 -1，表示初始时未计算过
        Arrays.fill(mem, -1);
        // 调用 dfs 方法从金额 amount 开始进行深度优先搜索
        int ans = dfs(amount, coins);
        // 如果 dfs 方法返回 100010，表示无法凑齐金额，返回 -1；否则返回 dfs 方法的结果
        return ans == 100010 ? -1 : ans;
    }

    // mem 备忘录数组，用于存储已经计算过的金额所需的最少硬币数量
    int[] mem;

    // dfs 方法是一个递归方法，用于计算凑齐剩余金额 rest 所需的最少硬币数量
    private int dfs(int rest, int[] coins) {
        // 如果剩余金额为 0，则不需要硬币，返回 0
        if (rest == 0) {
            return 0;
        }
        // 如果备忘录中已经计算过剩余金额 rest 的结果，则直接返回该结果
        if (mem[rest] != -1) {
            return mem[rest];
        }
        // 初始化 ans 为一个较大的数，用于存储凑齐当前剩余金额的最小硬币数量
        int ans = 100010;
        // 遍历所有可用的硬币面额
        for (int coin : coins) {
            // 如果当前硬币面额小于或等于剩余金额，则递归计算凑齐剩余金额减去该硬币面额所需的硬币数量
            // 并更新 ans 为当前硬币数量加一与已计算的最小硬币数量的较小值
            if (rest >= coin) {
                ans = Math.min(ans, dfs(rest - coin, coins) + 1);
            }
        }
        // 将计算得到的凑齐剩余金额所需的最小硬币数量存储到备忘录 mem 中
        mem[rest] = ans;
        // 返回凑齐剩余金额所需的最小硬币数量
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        @cache
        def dfs(cur):
            if cur == amount: return 0
            ans = inf
            for coin in coins:
                if coin + cur <= amount: ans = min(ans, dfs(coin + cur) + 1)
            return ans

        ans = dfs(0)
        return -1 if ans > amount else ans

零钱兑换 II

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

示例 1：

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2：

输入：amount = 3, coins = [2]
输出：0
解释：只用面额 2 的硬币不能凑成总金额 3 。

示例 3：

输入：amount = 10, coins = [10]
输出：1

提示：
1 <= coins.length <= 300
1 <= coins[i] <= 5000
coins 中的所有值 互不相同
0 <= amount <= 5000

题目解析

此题我们考虑使用“完全背包”的思想来做，当然，我们本章讲的是记忆化搜索，因此我们还是采用递归来实现这道题。

题目解析

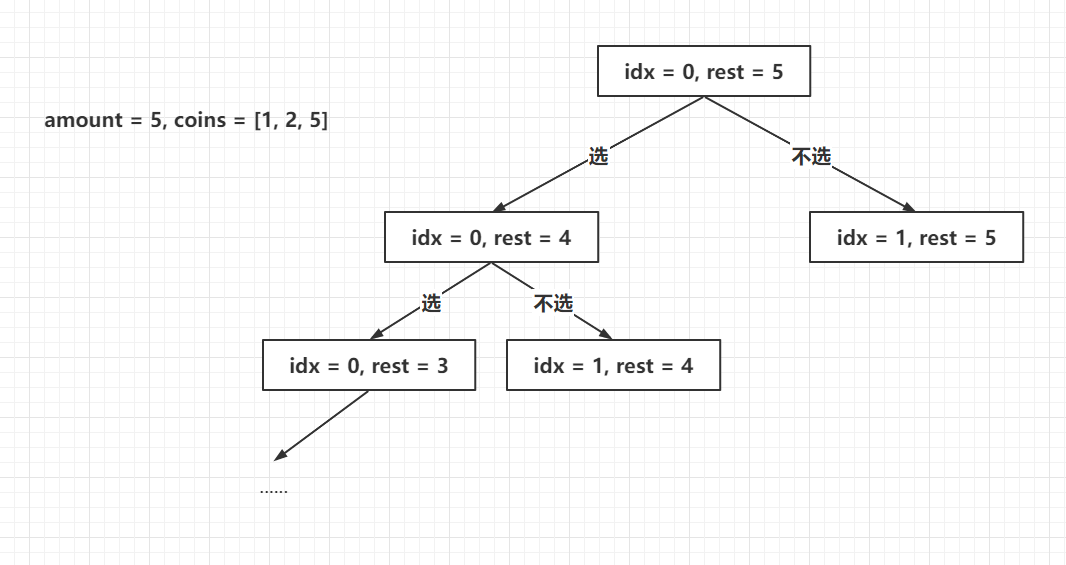
我们挨个硬币考虑，每个硬币有两种选择，要么选，要么不选，如果选的话下一次递归可以继续当前这个硬币。表达式如下：

f(i, j) = f(i, j - coins[i]) + f(i + 1, j)

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    /**
     * 计算兑换指定金额所需的硬币组合数量
     * @param amount 要兑换的金额
     * @param coins 可用的硬币面值数组
     * @return 组合数量
     */
    public int change(int amount, int[] coins) {
        // 初始化记忆化数组，用于存储计算过的结果
        mem = new int[coins.length][amount + 1];
        // 将记忆化数组初始化为-1，表示未计算过
        for (int i = 0 ; i < coins.length ; i++) Arrays.fill(mem[i], -1);
        // 调用深度优先搜索方法，开始计算组合数量
        return dfs(0, 0, amount, coins);
    }
    
    int[][] mem; // 记忆化数组，存储计算过的结果
    
    /**
     * 深度优先搜索方法，计算组合数量
     * @param idx 当前硬币的索引
     * @param sum 当前组合的金额总和
     * @param amount 目标金额
     * @param coins 可用的硬币面值数组
     * @return 组合数量
     */
    private int dfs(int idx, int sum, int amount, int[] coins) {
        // 如果当前金额总和大于等于目标金额，或者硬币索引超出范围，则返回
        if (sum >= amount || idx >= coins.length) return sum == amount ? 1 : 0;
        // 如果当前结果已经计算过，则直接返回该结果
        if (mem[idx][sum] != -1) return mem[idx][sum];
        // 递归调用深度优先搜索，分别考虑不选当前硬币和选取当前硬币两种情况
        int ans = dfs(idx + 1, sum, amount, coins) + dfs(idx, sum + coins[idx], amount, coins);
        // 将计算得到的结果存入记忆化数组
        mem[idx][sum] = ans;
        return ans;
    }
}

1
2
3
4
5
6
7
8
9
class Solution:
    def change(self, amount: int, coins: List[int]) -> int:
        @cache
        def dfs(i, Sum):
            if Sum >= amount or i >= len(coins):
                return 1 if Sum == amount else 0
            return dfs(i+1,Sum) + dfs(i, Sum + coins[i])
        return dfs(0, 0)

整数拆分

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

示例 1:

输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

提示:
2 <= n <= 58

题目解析

递归的思路：将 n 进行拆分，枚举所有的可能并且取最大值即可。

比如 n = 10，我们可以选择拆成 1+9 ，或者将 9 继续拆分，也可以选择 2+8，或者将 8 继续拆分，也就是表达式如下：

f(i) = max(j * (n - j), j * f(n - j))

其中，j∈[1,i−2]j \in [1,i - 2] 。

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    int[] mem; // 记忆化数组，用于存储计算过的结果
    
    /**
     * 计算整数拆分的最大乘积
     * @param n 待拆分的整数
     * @return 最大乘积
     */
    public int integerBreak(int n) {
        // 初始化记忆化数组
        this.mem = new int[n + 1];
        Arrays.fill(mem, -1);
        // 调用深度优先搜索方法进行计算
        return dfs(n);
    }
    
    /**
     * 深度优先搜索方法，计算整数拆分的最大乘积
     * @param n 待拆分的整数
     * @return 最大乘积
     */
    public int dfs(int n) {
        // 如果待拆分的整数为2，返回1（特殊情况）
        if (n == 2)
            return 1;
        // 如果计算过该值，则直接返回之前计算的结果
        if (mem[n] != 0)
            return mem[n];
        int res = 0; // 初始化最大乘积
        // 遍历拆分方案，计算最大乘积
        for (int i = 1; i <= n - 2; i++) {
            // 计算当前拆分方案的乘积，并取最大值
            res = Math.max(res, Math.max(i * (n - i), dfs(n - i) * i));
        }
        // 将计算得到的结果存入记忆化数组
        mem[n] = res;
        return res;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def integerBreak(self, n: int) -> int:
        @cache
        def dfs(i):
            if i == 2: return 1
            res = 0
            for j in range(1, i//2 + 1):
                res = max(res, j*(i-j), dfs(i-j)*j)
            return res

        return dfs(n)

买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：
1 <= prices.length <= 10^5
0 <= prices[i] <= 10^4

题目解析

我们可以选择两个状态来进行递归，一个状态idx是当前是哪一天，一个状态s是当前买卖股票的状态（可以选择用一个整型数来表示，0表示还没买，1表示手头有股票，可以卖了）

因此：

  • 当s是0的时候，我们可以选择买或者不动，如果选择买，则从0->1
  • 当s是1的时候，我们可以选择卖或者不动，如果选择卖，则从1->2

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {

    public int maxProfit(int[] prices) {
        // 初始化记忆化数组
        dp = new int[prices.length][2];
        // 将记忆化数组初始化为-1，表示未计算过
        for (int i = 0 ; i < prices.length ; i++) Arrays.fill(dp[i], -1);
        // 调用深度优先搜索方法开始计算最大利润
        return dfs(0, 0, prices);
    }
    
    int[][] dp; // 记忆化数组，存储计算过的结果
    
    /**
     * 深度优先搜索方法，计算最大利润
     * @param idx 当前天数的索引
     * @param s 当前持有股票的状态，0表示未持有，1表示持有
     * @param prices 股票价格数组
     * @return 最大利润
     */
    int dfs(int idx, int s, int[] prices) {
        // 如果已经遍历完所有天数或者已经交易了两次，则返回0
        if (idx == prices.length || s == 2) return 0;
        // 如果当前状态已经计算过，则直接返回之前计算的结果
        if (dp[idx][s] != -1) return dp[idx][s];
        // 如果当前状态为未持有股票
        if (s == 0) {
            // 取当前不持有股票与买入股票两种情况的最大利润
            return dp[idx][s] = Math.max(dfs(idx + 1, s, prices), dfs(idx + 1, s + 1, prices) - prices[idx]);
        }
        // 如果当前状态为持有股票
        // 取当前持有股票与卖出股票两种情况的最大利润
        return dp[idx][s] = Math.max(dfs(idx + 1, s, prices), dfs(idx + 1, s + 1, prices) + prices[idx]);
    }
}

买卖股票的最佳时机 II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

提示：
1 <= prices.length <= 3 * 10^4
0 <= prices[i] <= 10^4

题目解析

与上一个题目的区别在于这个题目是不限制买卖的次数的。

思路与上一题一致，一样选择两个状态来进行递归，一个状态idx是当前是哪一天，一个状态s是当前买卖股票的状态（可以选择用一个整型数来表示，0表示还没买，1表示手头有股票，可以卖了）

但是状态s的转换规则不一样

  • 当s是0的时候，我们可以选择买或者不动，如果选择买，则从0->1。
  • 当s是1的时候，我们可以选择卖或者不动，如果选择卖，则从1->0，正因为这个点，我们才可以实现重复买卖的操作（买了可以卖，卖了可以买……）

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {

    public int maxProfit(int[] prices) {
        // 初始化记忆化数组
        dp = new int[prices.length][2];
        // 将记忆化数组初始化为-1，表示未计算过
        for (int i = 0; i < prices.length; i++) Arrays.fill(dp[i], -1);
        // 调用深度优先搜索方法开始计算最大利润
        return dfs(0, 0, prices);
    }
    
    int[][] dp; // 记忆化数组，存储计算过的结果
    
    /**
     * 深度优先搜索方法，计算最大利润
     * @param idx 当前天数的索引
     * @param s 当前持有股票的状态，0表示未持有，1表示持有
     * @param prices 股票价格数组
     * @return 最大利润
     */
    int dfs(int idx, int s, int[] prices) {
        // 如果已经遍历完所有天数，则返回0
        if (idx == prices.length) return 0;
        // 如果当前状态已经计算过，则直接返回之前计算的结果
        if (dp[idx][s] != -1) return dp[idx][s];
        // 如果当前状态为未持有股票
        if (s == 0) {
            // 取当前不持有股票与买入股票两种情况的最大利润
            return dp[idx][s] = Math.max(dfs(idx + 1, s, prices), dfs(idx + 1, 1, prices) - prices[idx]);
        }
        // 如果当前状态为持有股票
        // 取当前持有股票与卖出股票两种情况的最大利润
        return dp[idx][s] = Math.max(dfs(idx + 1, s, prices), dfs(idx + 1, 0, prices) + prices[idx]);
    }
}

买卖股票的最佳时机 III

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入：prices = [3,3,5,0,0,3,1,4]
输出：6
解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这个情况下, 没有交易完成, 所以最大利润为 0。

示例 4：

输入：prices = [1]
输出：0

提示：
1 <= prices.length <= 105
0 <= prices[i] <= 105

题目解析

这个题的要求在于：买卖2次。思路依然沿用前两道题，区别在于：状态s我们从0->1, 1->2,2->3,3->4，分别表示：第一次买、第一次卖、第二次买、第二次卖。当s为4的时候停止递归，表示两次买卖完成。

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {

    // maxProfit 方法用于计算在给定价格数组 prices 下的最大利润
    // 可以进行多次买卖操作，但卖出后不能立即买入
    public int maxProfit(int[] prices) {
        // 初始化一个二维动态规划数组 dp，用于存储中间结果
        dp = new int[prices.length][4];
        // 使用 Arrays.fill 方法将 dp 填入 -1，表示初始时未计算过
        for (int i = 0; i < prices.length; i++) {
            Arrays.fill(dp[i], -1);
        }
        // 调用 dfs 方法从索引 0 开始进行递归计算
        return dfs(0, 0, prices);
    }

    // dp 二维数组，用于存储动态规划的中间结果
    int[][] dp;

    // dfs 方法是一个递归方法，用于计算在给定价格数组 prices 下的最大利润
    int dfs(int idx, int s, int[] prices) {
        // 如果索引 idx 已经到达数组末尾，或者已经进行了 4 次买卖操作，则无法再进行操作，返回 0
        if (idx == prices.length || s == 4) {
            return 0;
        }
        // 如果 dp 数组中当前状态的值已经计算过，则直接返回该值
        if (dp[idx][s] != -1) {
            return dp[idx][s];
        }
        // 如果 s 为 0 或 2，表示当前手中无股票，可以选择买入或等待一天
        if (s == 0 || s == 2) {
            // 计算买入或等待一天后的最大利润，并存储到 dp 中
            return dp[idx][s] = Math.max(dfs(idx + 1, s, prices), dfs(idx + 1, s + 1, prices) - prices[idx]);
        }
        // 如果 s 为 1 或 3，表示当前手中有股票，可以选择卖出或等待一天
        return dp[idx][s] = Math.max(dfs(idx + 1, s, prices), dfs(idx + 1, s + 1, prices) + prices[idx]);
    }
}

买卖股票的最佳时机 IV

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1：

输入：k = 2, prices = [2,4,1]
输出：2
解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2：

输入：k = 2, prices = [3,2,6,5,0,3]
输出：7
解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

提示：
0 <= k <= 100
0 <= prices.length <= 1000
0 <= prices[i] <= 1000

题目解析

依然沿用前几道题的思路，只是状态s发生改变，0->1, 1->2, 2->3…… 2k-1 -> 2k。分别表示第一次买、第一次卖….第k次买，第k次卖。

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {

    public int maxProfit(int k, int[] prices) {
        // 初始化记忆化数组
        dp = new int[prices.length][2 * k];
        // 将记忆化数组初始化为-1，表示未计算过
        for (int i = 0 ; i < prices.length ; i++) Arrays.fill(dp[i], -1);
        // 调用深度优先搜索方法开始计算最大利润
        return dfs(0, 0, prices, k);
    }
    
    int[][] dp; // 记忆化数组，存储计算过的结果
    
    /**
     * 深度优先搜索方法，计算最大利润
     * @param idx 当前天数的索引
     * @param s 当前持有股票的状态，0表示未持有，1表示持有
     * @param prices 股票价格数组
     * @param k 最多允许完成的交易次数
     * @return 最大利润
     */
    int dfs(int idx, int s, int[] prices, int k) {
        // 如果已经遍历完所有天数或者已经完成了允许的交易次数，则返回0
        if (idx == prices.length || s == 2 * k) return 0;
        // 如果当前状态已经计算过，则直接返回之前计算的结果
        if (dp[idx][s] != -1) return dp[idx][s];
        // 如果当前状态为未持有股票
        if (s % 2 == 0) {
            // 取当前不持有股票与买入股票两种情况的最大利润
            return dp[idx][s] = Math.max(dfs(idx + 1, s, prices, k), dfs(idx + 1, s + 1, prices, k) - prices[idx]);
        }
        // 如果当前状态为持有股票
        // 取当前持有股票与卖出股票两种情况的最大利润
        return dp[idx][s] = Math.max(dfs(idx + 1, s, prices, k), dfs(idx + 1, s + 1, prices, k) + prices[idx]);
    }
}

买卖股票的最佳时机含手续费

给定一个整数数组 prices，其中 prices[i] 表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

示例 1：

输入：prices = [1, 3, 2, 8, 4, 9], fee = 2
输出：8
解释：能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8

示例 2：

输入：prices = [1,3,7,5,10,3], fee = 3
输出：6

提示：
1 <= prices.length <= 5 * 10^4
1 <= prices[i] < 5 * 10^4
0 <= fee < 5 * 10^4

题目解析

此题相当于“买卖股票的最佳时机Ⅱ”的升级版，加入了手续费的概念，因此整体思路一致，只需要在每次卖的时候减去手续费即可。

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    // maxProfit 方法用于计算在给定价格数组 prices 和每次交易费用 fee 下的最大利润
    // 使用动态规划和递归的方法来解决问题
    public int maxProfit(int[] prices, int fee) {
        // 初始化一个二维动态规划数组 dp，行数为 prices 长度，列数为 2
        // 第一列表示手中无股票的情况，第二列表示手中有股票的情况
        dp = new int[prices.length][2];
        // 使用 Arrays.fill 方法将 dp 填入 -1，表示初始时未计算过
        for (int i = 0; i < prices.length; i++) {
            Arrays.fill(dp[i], -1);
        }
        // 调用 dfs 方法从索引 0 开始进行递归计算
        return dfs(0, 0, prices, fee);
    }

    // dp 二维数组，用于存储动态规划的中间结果
    int[][] dp;

    // dfs 方法是一个递归方法，用于计算在给定价格数组 prices 和交易费用 fee 下的最大利润
    int dfs(int idx, int s, int[] prices, int fee) {
        // 如果索引 idx 已经到达 prices 数组的末尾，则无法再进行交易，返回 0
        if (idx == prices.length) {
            return 0;
        }
        // 如果 dp 数组中当前状态的值已经计算过，则直接返回该值
        if (dp[idx][s] != -1) {
            return dp[idx][s];
        }
        // 如果当前状态 s 为 0，表示手中无股票
        if (s == 0) {
            // 可以选择不操作或买入股票
            // 递归计算不操作或买入股票后的最大利润，并存储到 dp 中
            return dp[idx][s] = Math.max(dfs(idx + 1, s, prices, fee), dfs(idx + 1, s + 1, prices, fee) - prices[idx]);
        }
        // 如果当前状态 s 为 1，表示手中有股票
        // 可以选择卖出股票或不操作
        // 递归计算卖出股票或不操作后的最大利润，并存储到 dp 中
        // 注意卖出股票后的费用 fee 需要从利润中扣除
        return dp[idx][s] = Math.max(dfs(idx + 1, s, prices, fee), dfs(idx + 1, 0, prices, fee) + prices[idx] - fee);
    }
}

最佳买卖股票时机含冷冻期

给定一个整数数组 prices，其中第 prices[i] 表示第 i 天的股票价格 。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

示例 2:

输入: prices = [1]
输出: 0

提示：
1 <= prices.length <= 5000
0 <= prices[i] <= 1000

题目解析

此题相当于“买卖股票的最佳时机Ⅱ”的升级版，加入了冷却期的概念，因此整体思路一致，只需要在每次卖的时候跳过一天即可。

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    // maxProfit 方法用于计算在给定价格数组 prices 下的最大利润
    // 允许无限次买卖，但卖出股票后不能立即买入
    public int maxProfit(int[] prices) {
        // 初始化一个二维动态规划数组 dp，行数为 prices 长度，列数为 2
        // 第一列表示手中无股票，第二列表示手中有股票
        dp = new int[prices.length][2];
        // 使用 Arrays.fill 方法将 dp 填入 -1，表示初始时未计算过
        for (int i = 0; i < prices.length; i++) {
            Arrays.fill(dp[i], -1);
        }
        // 调用 dfs 方法从索引 0 开始进行递归计算
        return dfs(0, 0, prices);
    }

    // dp 二维数组，用于存储动态规划的中间结果
    int[][] dp;

    // dfs 方法是一个递归方法，用于计算在给定价格数组 prices 下的最大利润
    int dfs(int idx, int s, int[] prices) {
        // 如果索引 idx 大于等于 prices 的长度，表示已经到达最后一天，无法再进行交易，返回 0
        if (idx >= prices.length) {
            return 0;
        }
        // 如果 dp 数组中当前状态的值已经计算过，则直接返回该值
        if (dp[idx][s] != -1) {
            return dp[idx][s];
        }
        // 如果当前状态 s 为 0，表示手中无股票
        if (s == 0) {
            // 可以选择不操作或买入股票
            // 递归计算不操作或买入股票后的最大利润，并存储到 dp 中
            // 注意买入股票后，需要减去当前的价格
            return dp[idx][s] = Math.max(dfs(idx + 1, s, prices), dfs(idx + 1, 1, prices) - prices[idx]);
        }
        // 如果当前状态 s 为 1，表示手中有股票
        // 可以选择卖出股票或不操作
        // 由于卖出股票后不能立即买入，因此需要跳过下一天（即 idx + 2）
        // 递归计算卖出股票或不操作后的最大利润，并存储到 dp 中
        // 注意卖出股票后，需要加上当前的价格
        return dp[idx][s] = Math.max(dfs(idx + 1, s, prices), dfs(idx + 2, 0, prices) + prices[idx]);
    }
}
计算机基础 > 算法
#算法
算法训练3.1 单调栈自顶向下的动态规划（记忆化搜索）第二部分
https://fulequn.github.io/2024/05/Article202405121/
作者
Fulequn
发布于
2024年5月12日
许可协议