算法训练-6高效算法部分 单调栈

6.4 单调栈

单调栈是一种基于栈的数据结构，所谓的单调就是满足单调递增（单调递减）的栈。主要用于解决 next_greater 问题，也就是找到下一个更大的元素。

基本模板如下：

1
2
3
4
5
6
7
8
stack;//单调栈
for (int i = 0 ; i < n ; i++) {
    while (stack && nums[stack.top] < nums[i]) {
        int top = stack.pop();
        //此时说明 nums[top]的下一个更大的元素为nums[i]
    }
    stack.push(i);
}

每日温度

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]

示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]

提示：
1 <= temperatures.length <= 10530 <= temperatures[i] <= 100

题目解析

此题比较简单，属于单调栈的模板题。目的也是简单的找到一个更大的元素的位置。

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {

    // dailyTemperatures 方法用于根据每日温度数组 temperatures 找出需要多少天会更热
    // 返回一个数组，其中第 i 位的值表示从第 i 天开始需要多少天温度会首次高于当天
    public int[] dailyTemperatures(int[] temperatures) {
        // 使用 Deque 和 LinkedList 来实现一个栈结构，用于存储索引
        Deque<Integer> stack = new LinkedList<>();
        // 创建一个与输入数组 temperatures 等长的数组 res 用于存储结果
        int[] res = new int[temperatures.length];
        
        // 遍历 temperatures 数组
        for (int i = 0; i < temperatures.length; i++) {
            // 当栈不为空且当前温度高于栈顶元素对应的温度时，执行循环体
            while (!stack.isEmpty() && temperatures[stack.getLast()] < temperatures[i]) {
                // 弹出栈顶元素，即找到第一个温度低于当前温度的天数的索引
                int top = stack.pollLast();
                // 计算从栈顶元素对应的天数到当前天数的天数差，并存储在结果数组 res 中
                res[top] = i - top;
            }
            // 将当前遍历到的天数的索引压入栈中
            stack.addLast(i);
        }
        
        // 返回结果数组 res
        return res;
    }
}

下一个更大元素 I

nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。

给你两个 没有重复元素 的数组 nums1 和 nums2 ，下标从 0 开始计数，其中 nums1 是 nums2 的子集。

对于每个 0 <= i < nums1.length ，找出满足 nums1[i] == nums2[j] 的下标 j ，并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素，那么本次查询的答案是 -1 。

返回一个长度为 nums1.length 的数组 ans 作为答案，满足 ans[i] 是如上所述的 下一个更大元素 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
示例 1：
输入：nums1 = [4,1,2], nums2 = [1,3,4,2].
输出：[-1,3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 4 ，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。
- 1 ，nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ，nums2 = [1,3,4,2]。不存在下一个更大元素，所以答案是 -1 。

示例 2：
输入：nums1 = [2,4], nums2 = [1,2,3,4].
输出：[3,-1]
解释：nums1 中每个值的下一个更大元素如下所述：
- 2 ，nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ，nums2 = [1,2,3,4]。不存在下一个更大元素，所以答案是 -1 。

提示：
1 <= nums1.length <= nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 10^4
nums1和nums2中所有整数 互不相同
nums1 中的所有整数同样出现在 nums2 中

题目解析

此题是找到nums1[i]对应的元素在nums2中找到下一个更大的元素，典型的单调栈模板题。大体思路如下：

  • 统计nums2中每个元素对应的“下一个更大的元素”
  • 遍历nums1，找到nums1中每个元素对应的答案。

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {

    // nextGreaterElement 方法用于找出数组 nums1 中每个元素的第一个更大的元素在数组 nums2 中的位置
    // 如果不存在，则该位置为 -1
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        // 使用 Deque 和 LinkedList 来实现一个栈结构，用于存储索引
        Deque<Integer> stack = new LinkedList<>();
        // 使用 HashMap 来存储 nums2 中每个元素的下一个更大元素的值
        HashMap<Integer, Integer> map = new HashMap<>();
        
        // 遍历数组 nums2
        for (int i = 0; i < nums2.length; i++) {
            // 当栈不为空且栈顶元素对应的值小于当前元素的值时，执行循环体
            while (!stack.isEmpty() && nums2[stack.peekLast()] < nums2[i]) {
                // 弹出栈顶元素，即找到当前元素前一个更小的元素的索引
                int top = stack.pollLast();
                // 将栈顶元素对应的值和当前元素的值作为键值对存入 map 中
                map.put(nums2[top], nums2[i]);
            }
            // 将当前遍历到的元素的索引压入栈中
            stack.addLast(i);
        }
        
        // 初始化结果数组 res，其长度与 nums1 相同
        int[] res = new int[nums1.length];
        // 遍历数组 nums1
        for (int i = 0; i < nums1.length; i++) {
            // 使用 getOrDefault 方法从 map 中获取 nums1[i] 对应的下一个更大元素的值
            // 如果 map 中不存在 nums1[i]，则结果为 -1
            res[i] = map.getOrDefault(nums1[i], -1);
        }
        
        // 返回结果数组 res
        return res;
    }
}

下一个更大元素 II

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

1
2
3
4
5
6
7
8
9
10
11
12
13
示例 1:
输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

示例 2:
输入: nums = [1,2,3,4,3]输出: [2,3,4,-1,4]

提示:

1 <= nums.length <= 10^4
-10^9 <= nums[i] <= 10^9

题目解析

此题也是单调栈的模板应用，除了一个点：循环数组。也就是我们需要对循环数组加以处理即可。

处理循环数组的思路如下：我们把数组想象成两个数组相加，如 [1,2,1]，我们当成[1,2,1,1,2,1]。如此一来我们只需要对新的数组找到next_greater即可，结果应该为[2,-1,2,2,-1,-1]，我们只要截取前半部分即可。实际写代码的过程并不需要真正创建两倍的数组，按照思路进行处理即可。新数组中的元素下标对应到原数组的下标应该 mod nums.length即可。

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {

    // nextGreaterElements 方法用于找出数组 nums 中每个元素的下一个更大元素
    // 如果不存在下一个更大元素，则对应位置的值为 -1
    public int[] nextGreaterElements(int[] nums) {
        // 初始化结果数组 res，其长度与 nums 相同，并将所有元素填充为 -1
        int[] res = new int[nums.length];
        Arrays.fill(res, -1);
        
        // 初始化一个栈结构，用于存储索引
        Deque<Integer> stack = new LinkedList<>();
        
        // 遍历数组，次数为 nums 长度的两倍，以处理数组循环遍历的情况
        for (int i = 0; i < 2 * nums.length; i++) {
            // 当栈不为空且栈顶元素对应的数值小于当前元素的数值时，执行循环体
            while (!stack.isEmpty() && nums[stack.getLast() % nums.length] < nums[i % nums.length]) {
                // 从栈中弹出一个元素，该元素是当前元素之前一个更小元素的索引
                int top = stack.pollLast();
                // 如果弹出的索引小于 nums 的长度，则说明该索引是 nums 的有效索引
                // 将当前索引 i 对应的元素值赋给结果数组 res 中的 top 索引位置
                if (top < nums.length) {
                    res[top] = nums[i % nums.length];
                }
            }
            // 将当前索引 i 添加到栈中，用于后续查找下一个更大元素
            stack.addLast(i);
        }
        
        // 返回结果数组 res，其中存储了每个元素的下一个更大元素的索引
        return res;
    }
}

去除重复字母

给你一个字符串 s ，请你去除字符串中重复的字母，使得每个字母只出现一次。需保证 返回结果的字典序最小（要求不能打乱其他字符的相对位置）。

1
2
3
4
5
6
7
8
9
10
11
示例 1：
输入：s = “bcabc”
输出：“abc”

示例 2：
输入：s = “cbacdcbc”
输出：“acdb”

提示：
1 <= s.length <= 10^4
s 由小写英文字母组成

题目解析

此题属于比较有难度的单调栈优化的题目。如何找到字典序最小的字符串呢？很明显应该是尽量使得字典序单调递增。我们以样例1进行举例：我们不断往后选取字符的过程如下：

  • b
  • bc【因为bc满足单调上升】
  • bca，此时a不满足单调上升，并且 c在a后面还有出现，因此我们可以选择删除c，因此得到的是ba
  • 由于ba不满足单调上升并且b在a后面还有出现，因此我们可以选择删除b，因此得到a
  • ab
  • abc

上述就是单调栈的过程，尽量使得栈中元素符合单调递增的关系，才可以使得字典序最小。

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {

    // removeDuplicateLetters 方法用于找出字符串 s 中的最小不重复子串
    public String removeDuplicateLetters(String s) {
        // 使用一个栈结构来存储不重复子串中字符的索引
        Deque<Integer> stack = new LinkedList<>();
        // 使用一个整型数组 cnter 来统计从索引 i 往后每个字符还剩余的次数
        int[] cnter = new int[26];
        // 将字符串 s 转换为字符数组 cs
        char[] cs = s.toCharArray();
        // 统计字符数组 cs 中每个字符出现的次数
        for (char c : cs) {
            cnter[c - 'a']++;
        }
        // 使用一个整型数组 map 来统计当前栈中已经出现的元素，避免出现重复
        int[] map = new int[26];
        // 遍历字符数组 cs
        for (int i = 0; i < cs.length; i++) {
            // 将当前字符的剩余次数减一
            cnter[cs[i] - 'a']--;
            // 如果当前字符已经在栈中出现过，则跳过当前循环
            if (map[cs[i] - 'a'] == 1) {
                continue;
            }
            // 当栈不为空且栈顶字符大于当前字符，并且当前字符在后面仍然出现，则弹出栈顶字符
            while (!stack.isEmpty() && cs[stack.getLast()] > cs[i] && cnter[cs[stack.getLast()] - 'a'] > 0) {
                int top = stack.pollLast();
                // 将弹出的字符标记为未出现过
                map[cs[top] - 'a'] = 0;
            }
            // 将当前字符标记为已出现过
            map[cs[i] - 'a'] = 1;
            // 将当前字符的索引压入栈中
            stack.addLast(i);
        }
        // 使用 StringBuilder 来构建最终的不重复子串
        StringBuilder sb = new StringBuilder();
        // 遍历栈，将栈中的字符按索引顺序拼接成字符串
        for (int c : stack) {
            sb.append(cs[c]);
        }
        // 返回构建好的不重复子串
        return sb.toString();
    }
}

柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

示例1

输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

示例2

输入： heights = [2,4]
输出： 4

提示：
1 <= heights.length <=10^5
0 <= heights[i] <= 10^4

题目解析

此题属于笔试、面试都非常高频的题目，但是难度比较大。

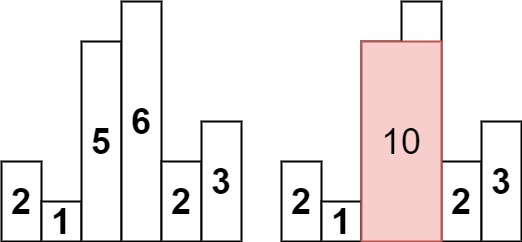
观察可知，最终答案肯定是会完整的包含某个柱子，也就是说以某个柱子作为高，我们只需要算宽即可，而宽就是该柱子左边的第一个比他小的值和右边第一个比他小的值这个区间内。比如样例1中倒数第二个柱子：

因此解题思路如下：

  • 统计每一个元素左边第一个比他小的元素的位置
  • 统计每一个元素右边第一个比他小的元素的位置
  • 遍历每一个柱子，统计最大值即可。

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution {

    // largestRectangleArea 方法用于计算给定数组 heights 中矩形的最大面积
    public int largestRectangleArea(int[] heights) {
        int n = heights.length; // 数组 heights 的长度
        // 初始化 rights 数组，用于存储每个高度值右边界的位置
        int[] rights = new int[n];
        Arrays.fill(rights, n); // 初始时，假设所有高度值的右边界都是 n
        
        // 使用一个栈结构来辅助计算右边界
        Deque<Integer> stack = new LinkedList<>();
        
        // 从左到右遍历 heights，计算右边界
        for (int i = 0; i < n; i++) {
            // 当栈不为空且当前高度值大于栈顶高度值时，栈顶元素出栈
            // 同时更新栈顶元素的右边界索引
            while (!stack.isEmpty() && heights[stack.getLast()] > heights[i]) {
                int top = stack.pollLast();
                rights[top] = i;
            }
            // 当前高度值进栈
            stack.addLast(i);
        }
        
        // 初始化 left 数组，用于存储每个高度值左边界的位置
        int[] left = new int[n];
        Arrays.fill(left, -1); // 初始时，假设所有高度值的左边界都是 -1
        
        // 清空栈，准备从右到左遍历 heights，计算左边界
        stack.clear();
        
        // 从右到左遍历 heights，计算左边界
        for (int i = n - 1; i >= 0; i--) {
            // 当栈不为空且当前高度值大于栈顶高度值时，栈顶元素出栈
            // 同时更新栈顶元素的左边界索引
            while (!stack.isEmpty() && heights[stack.getLast()] > heights[i]) {
                int top = stack.pollLast();
                left[top] = i;
            }
            // 当前高度值进栈
            stack.addLast(i);
        }
        
        // 初始化结果 res 为 0
        int res = 0;
        
        // 计算每个高度值对应的矩形面积，并更新结果 res
        for (int i = 0; i < n; i++) {
            // 计算以 heights[i] 为高的矩形的宽度，即右边界索引减去左边界索引再减去 1
            // 然后计算面积，更新结果 res
            res = Math.max(res, (rights[i] - left[i] - 1) * heights[i]);
        }
        
        // 返回计算出的矩形的最大面积
        return res;
    }
}

接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

示例1

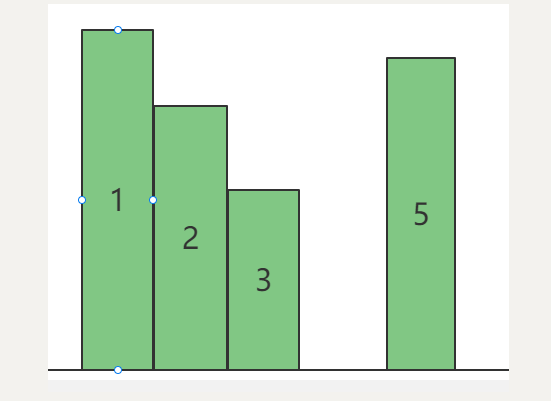
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：
n == height.length
1 <= n <= 2 * 10^4
0 <= height[i] <= 10^5

题目解析

此题也是面试笔试的高频题，也是具有比较大的难度。

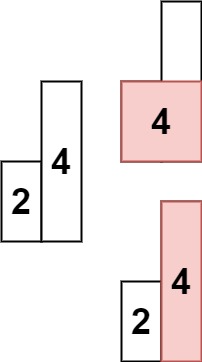
如果柱子一直是单调递减的，那么是不可能接的到雨水的，只有遇到单调递减后递增才会产生凹槽，才可以接到雨水。因此我们需要用单调栈来记录每一个柱子下一个更大的柱子的位置，在这个过程中进行计算。

能够接收雨水的数量取决于“凹槽”的面积，但是由于“凹槽”的形状可能是非矩形的，所以我们需要分层计算。

比如下图：

题解1

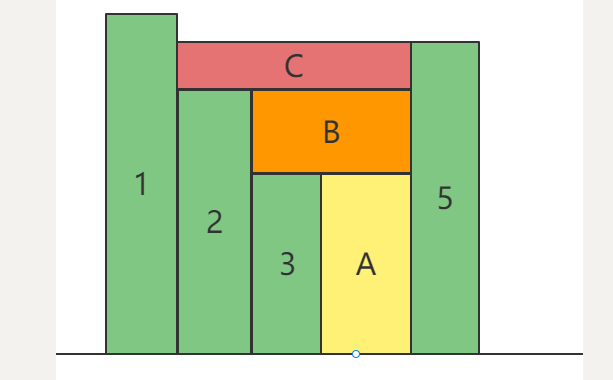
能够接雨水的多少我们划分成如下几部分：

题解2

其中，

A的体积为： （3号柱子的高度） * （5号柱子和3号柱子之间的距离）；B的体积为：（2号柱子的高度 - 3号柱子的高度） * （5号柱子和2号柱子之间的距离）；C的体积为：（1号柱子的高度 - 5号柱子的高度） * （5号柱子和1号柱子之间的距离）

C的体积的运算方式是不一样的，因为并不满足height[1] < height[5]；因此这里得做特殊处理。

代码展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {

    // trap 方法用于计算给定数组 height 中的梯形积水量
    // 数组 height 表示柱状图中各个柱子的高度
    public int trap(int[] height) {
        int ans = 0; // 初始化积水量的总和为 0
        Deque<Integer> stack = new LinkedList<>(); // 使用栈结构来存储索引
        int n = height.length; // 获取数组 height 的长度
        
        // 遍历数组 height 中的每个元素
        for (int i = 0; i < n; i++) {
            int last = 0; // 初始化 last 为 0，用于记录栈中记录的前一个高度值
            
            // 当栈不为空且栈顶元素对应的高度小于等于当前高度时，执行循环体
            while (!stack.isEmpty() && height[stack.getLast()] <= height[i]) {
                // 从栈中弹出一个元素，该元素是当前元素之前第一个高度小于当前高度的元素的索引
                int top = stack.pollLast();
                // 计算栈中元素与当前元素之间的积水量，并累加到 ans
                ans += (i - top - 1) * (height[top] - last);
                // 更新 last 为栈中弹出元素的高度
                last = height[top];
            }
            
            // 如果栈不为空，计算当前高度与栈顶高度之间的积水量，并累加到 ans
            if (!stack.isEmpty()) {
                ans += (i - stack.getLast() - 1) * (height[i] - last);
            }
            
            // 将当前索引 i 压入栈中，用于后续计算积水量
            stack.addLast(i);
        }
        
        // 返回积水量的总和 ans
        return ans;
    }
}
计算机基础 > 算法
#算法
算法训练-6高效算法部分 单调栈
https://fulequn.github.io/2024/05/Article202405071/
作者
Fulequn
发布于
2024年5月7日
许可协议