2024.2.17 Java基础（泛型+Set+数据结构）

*1 泛型

1.1 泛型概述

  • 泛型的介绍

    泛型是JDK5中引入的特性，它提供了编译时类型安全检测机制。

  • 泛型的好处

    1. 把运行时期的问题提前到了编译期间；
    2. 避免了强制类型转换。

  • 泛型的定义格式

    • <类型>: 指定一种类型的格式.尖括号里面可以任意书写,一般只写一个字母.例如: <E>、 <T>；
    • <类型1,类型2…>: 指定多种类型的格式,多种类型之间用逗号隔开.例如: <E,T>、 <K,V>。

2 Set集合

2.1 Set集合概述和特点

  • 不可以存储重复元素；
  • 没有索引，不能使用普通for循环遍历。

2.2 Set集合的使用

存储字符串并遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class MySet1 {
    public static void main(String[] args) {
      	//创建集合对象
        Set<String> set = new TreeSet<>();
      	//添加元素
        set.add("ccc");
        set.add("aaa");
        set.add("aaa");
        set.add("bbb");

//        for (int i = 0; i < set.size(); i++) {
//            //Set集合是没有索引的，所以不能使用通过索引获取元素的方法
//        }
      
      	//遍历集合
        Iterator<String> it = set.iterator();
        while (it.hasNext()){
            String s = it.next();
            System.out.println(s);
        }
        System.out.println("-----------------------------------");
        for (String s : set) {
            System.out.println(s);
        }
    }
}

*2.3 TreeSet集合

  • 不可以存储重复元素
  • 没有索引
  • 可以将元素按照规则进行排序
    • TreeSet()：根据其元素的自然排序进行排序
    • TreeSet(Comparator comparator) ：根据指定的比较器进行排序

2.3.1 自然排序Comparable的使用

  • 案例需求

    • 存储学生对象并遍历，创建TreeSet集合使用无参构造方法
    • 要求：按照年龄从小到大排序，年龄相同时，按照姓名的字母顺序排序

  • 实现步骤

    1. 使用空参构造创建TreeSet集合
      • 用TreeSet集合存储自定义对象，无参构造方法使用的是自然排序对元素进行排序的
    2. 自定义的Student类实现Comparable接口
      • 自然排序，就是让元素所属的类实现Comparable接口，重写compareTo(T o)方法
    3. 重写接口中的compareTo方法
      • 重写方法时，一定要注意排序规则必须按照要求的主要条件和次要条件来写

  • 代码实现

    学生类

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    public class Student implements Comparable<Student>{
        private String name;
        private int age;

        @Override
        public int compareTo(Student o) {
            //按照对象的年龄进行排序
            //主要判断条件: 按照年龄从小到大排序
            int result = this.age - o.age;
            //次要判断条件: 年龄相同时，按照姓名的字母顺序排序
            result = result == 0 ? this.name.compareTo(o.getName()) : result;
            return result;
        }
    }

    测试类

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    public class MyTreeSet2 {
        public static void main(String[] args) {
            //创建集合对象
            TreeSet<Student> ts = new TreeSet<>();
    	    //创建学生对象
            Student s1 = new Student("zhangsan",28);
            Student s2 = new Student("lisi",27);
            Student s3 = new Student("wangwu",29);
            Student s4 = new Student("zhaoliu",28);
            Student s5 = new Student("qianqi",30);
    		//把学生添加到集合
            ts.add(s1);
            ts.add(s2);
            ts.add(s3);
            ts.add(s4);
            ts.add(s5);
    		//遍历集合
            for (Student student : ts) {
                System.out.println(student);
            }
        }
    }

2.3.2 比较器排序Comparator的使用

  • 案例需求

    • 存储老师对象并遍历，创建TreeSet集合使用带参构造方法
    • 要求：按照年龄从小到大排序，年龄相同时，按照姓名的字母顺序排序

  • 实现步骤

    • 用TreeSet集合存储自定义对象，带参构造方法使用的是比较器排序对元素进行排序的
    • 比较器排序，就是让集合构造方法接收Comparator的实现类对象，重写compare(T o1,T o2)方法
    • 重写方法时，一定要注意排序规则必须按照要求的主要条件和次要条件来写

  • 代码实现

    老师类

    1
    2
    3
    4
    public class Teacher {
        private String name;
        private int age;
    }

    测试类

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    public class MyTreeSet4 {
        public static void main(String[] args) {
          	//创建集合对象
            TreeSet<Teacher> ts = new TreeSet<>(new Comparator<Teacher>() {
                @Override
                public int compare(Teacher o1, Teacher o2) {
                    //o1表示现在要存入的那个元素
                    //o2表示已经存入到集合中的元素
                  
                    //主要条件
                    int result = o1.getAge() - o2.getAge();
                    //次要条件
                    result = result == 0 ? o1.getName().compareTo(o2.getName()) : result;
                    return result;
                }
            });
    		//创建老师对象
            Teacher t1 = new Teacher("zhangsan",23);
            Teacher t2 = new Teacher("lisi",22);
            Teacher t3 = new Teacher("wangwu",24);
            Teacher t4 = new Teacher("zhaoliu",24);
    		//把老师添加到集合
            ts.add(t1);
            ts.add(t2);
            ts.add(t3);
            ts.add(t4);
    		//遍历集合
            for (Teacher teacher : ts) {
              System.out.println(teacher);
            }
      }
    }

2.3.3 两种比较方式总结

  • 两种比较方式小结
    • 自然排序: 自定义类实现Comparable接口，重写compareTo方法，根据返回值进行排序；
    • 比较器排序: 创建TreeSet对象的时候传递Comparator的实现类对象,重写compare方法,根据返回值进行排序；
    • 在使用的时候,默认使用自然排序,当自然排序不满足现在的需求时,必须使用比较器排序。
  • 两种方式中关于返回值的规则
    • 如果返回值为负数，表示当前存入的元素是较小值，存左边；
    • 如果返回值为0，表示当前存入的元素跟集合中元素重复了，不存；
    • 如果返回值为正数，表示当前存入的元素是较大值，存右边。

2.4 HashSet集合

2.4.1 HashSet集合概述和特点

  • 底层数据结构是哈希表；
  • 存取无序；
  • 不可以存储重复元素；
  • 没有索引,不能使用普通for循环遍历。
  • HashSet集合存储自定义类型元素,要想实现元素的唯一,要求必须重写hashCode方法和equals方法

*2.4.2 哈希值

  • 哈希值简介

    是JDK根据对象的地址或者字符串或者数字算出来的int类型的数值。

  • 如何获取哈希值

    Object类中的public int hashCode()：返回对象的哈希码值。

  • 哈希值的特点

    • 同一个对象多次调用hashCode()方法返回的哈希值是相同的；
    • 默认情况下，不同对象的哈希值是不同的。而重写hashCode()方法，可以实现让不同对象的哈希值相同。

*2.4.3 哈希表结构

  • JDK1.8以前

    ​ 数组 + 链表

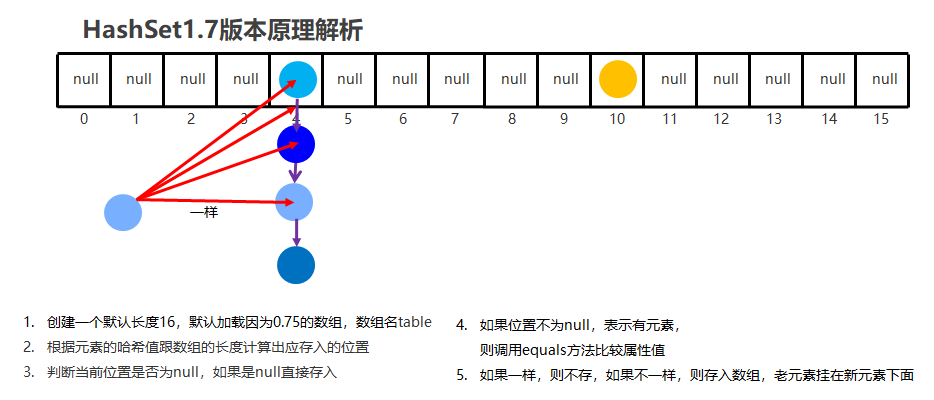
    14_JKD8以前哈希表

  • JDK1.8以后

    • 节点个数少于等于8个

      ​ 数组 + 链表

    • 节点个数多于8个

      ​ 数组 + 红黑树

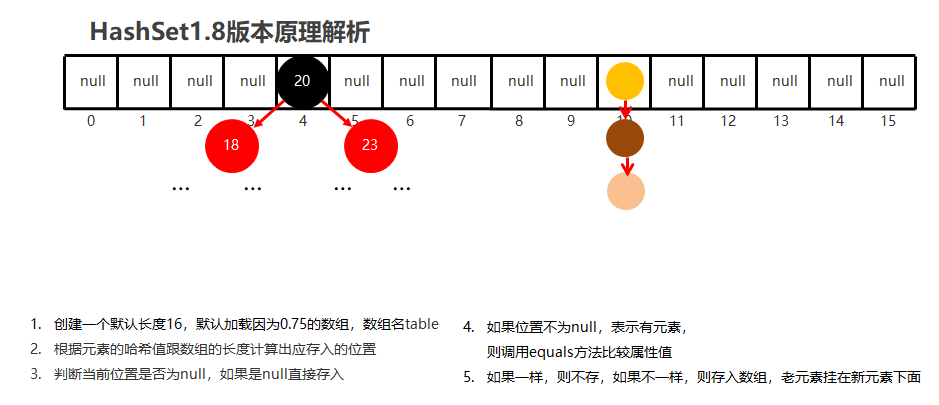
    15_JKD8以后哈希表

3 数据结构

3.1 二叉树

  • 二叉树的特点

    • 二叉树中,任意一个节点的度要小于等于2
      • 节点: 在树结构中,每一个元素称之为节点；
      • 度: 每一个节点的子节点数量称之为度。

  • 二叉树结构图

    01_二叉树结构图

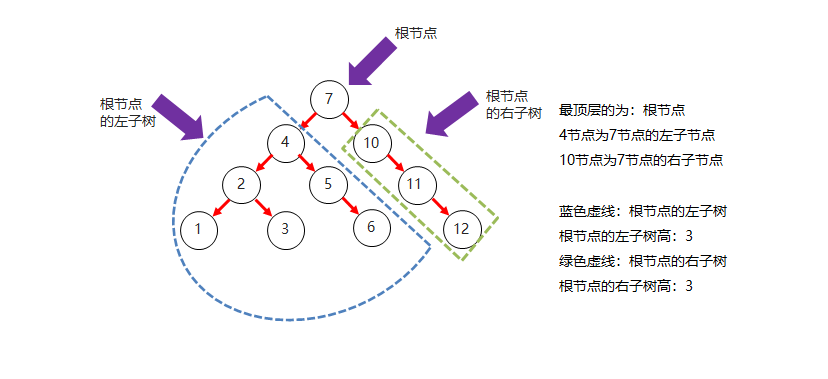
3.2 二叉查找树

  • 二叉查找树的特点

    • 二叉查找树,又称二叉排序树或者二叉搜索树；
    • 每一个节点上最多有两个子节点；
    • 左子树上所有节点的值都小于根节点的值；
    • 右子树上所有节点的值都大于根节点的值。

  • 二叉查找树结构图

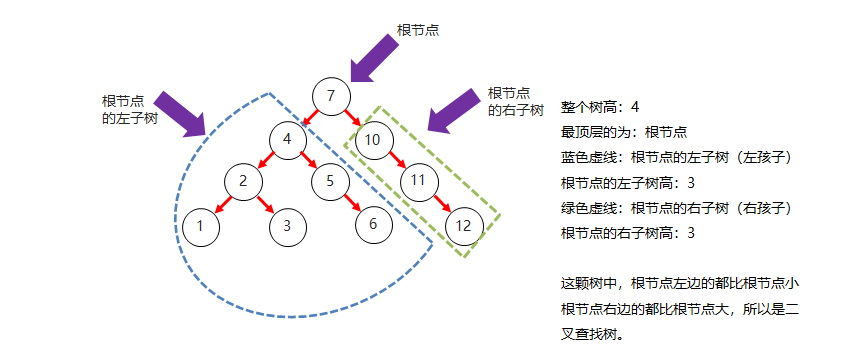
    02_二叉查找树结构图

  • 二叉查找树和二叉树对比结构图

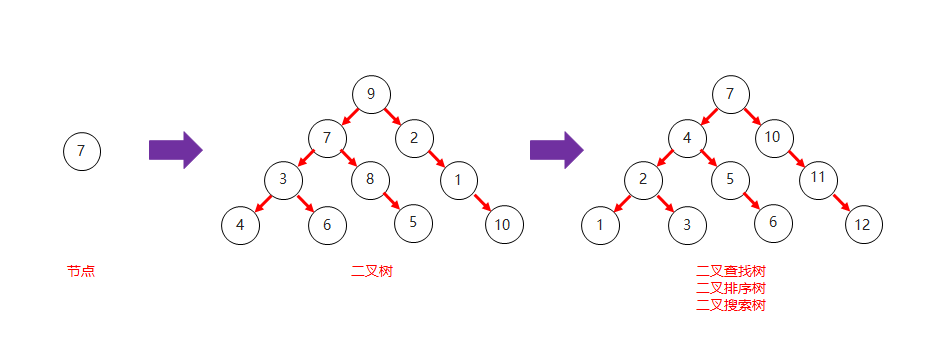
    03_二叉查找树和二叉树对比结构图

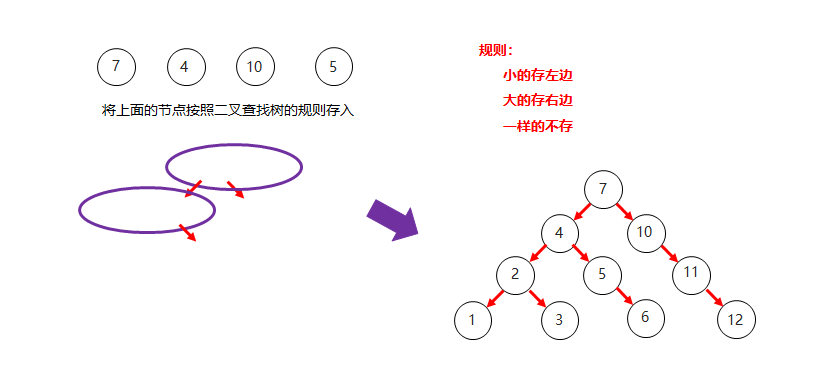
  • 二叉查找树添加节点规则

    • 小的存左边
    • 大的存右边
    • 一样的不存

    04_二叉查找树添加节点规则

*3.3 平衡二叉树

  • 平衡二叉树的特点

    • 二叉树左右两个子树的高度差不超过1
    • 任意节点的左右两个子树都是一颗平衡二叉树

  • 平衡二叉树旋转

    • 旋转触发时机

      • 当添加一个节点之后,该树不再是一颗平衡二叉树。

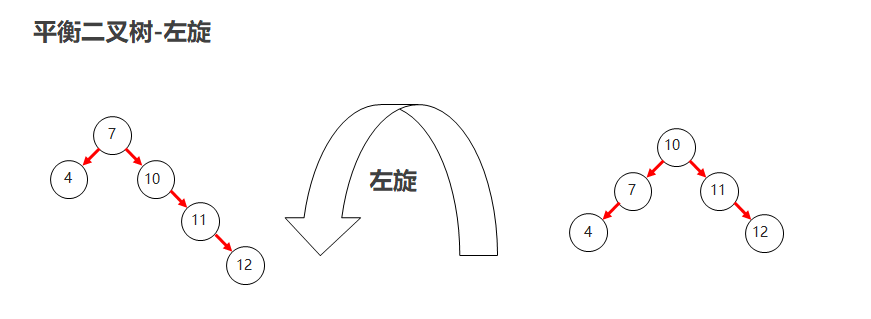
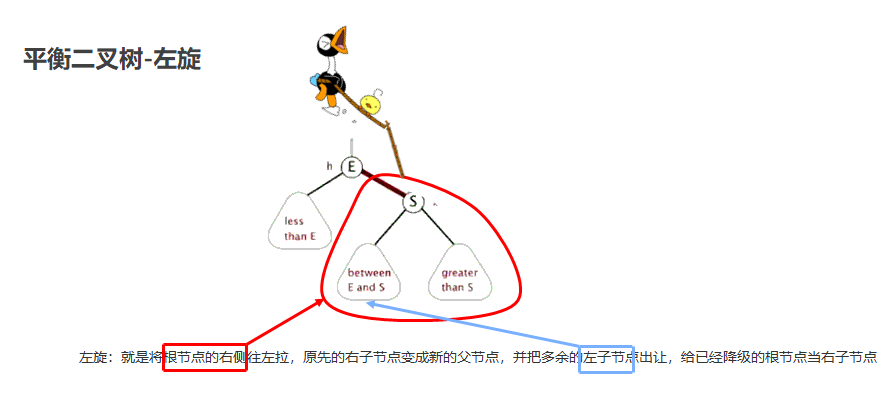
    • 左旋

      • 就是将根节点的右侧往左拉,原先的右子节点变成新的父节点,并把多余的左子节点出让,给已经降级的根节点当右子节点

      05_平衡二叉树左旋01

      05_平衡二叉树左旋02

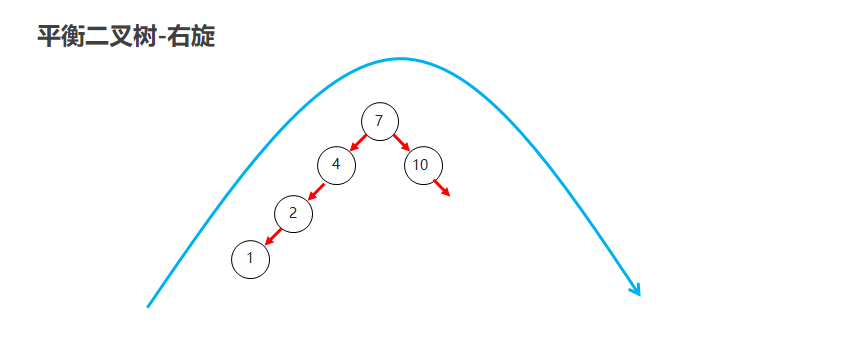
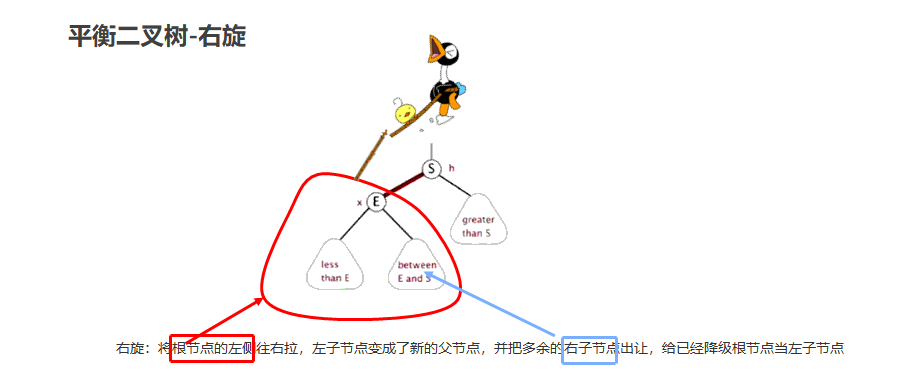
    • 右旋

      • 就是将根节点的左侧往右拉,左子节点变成了新的父节点,并把多余的右子节点出让,给已经降级根节点当左子节点

        06_平衡二叉树右旋01

        06_平衡二叉树右旋02

  • 平衡二叉树和二叉查找树对比结构图

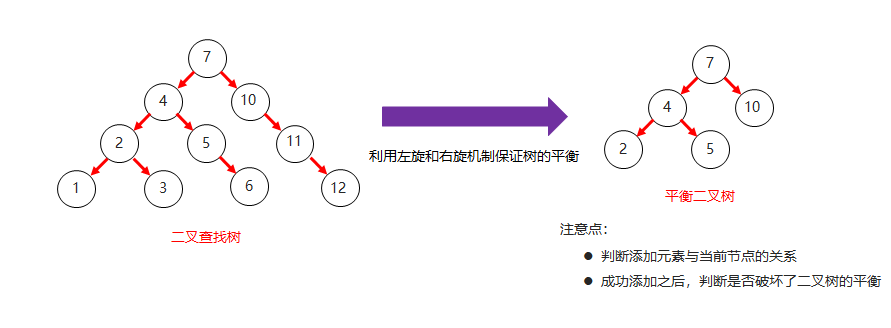
    07_平衡二叉树和二叉查找树对比结构图

  • 平衡二叉树旋转的四种情况

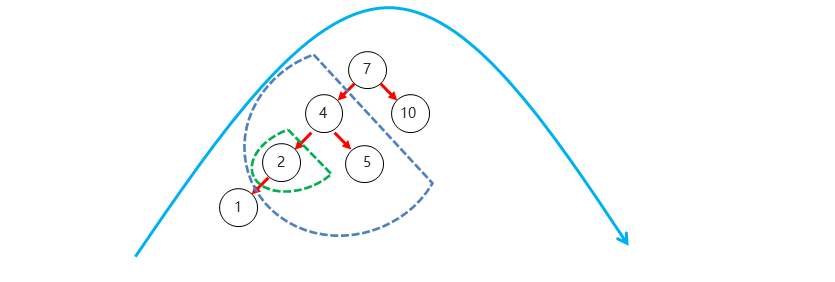
    • 左左

      • 左左: 当根节点左子树的左子树有节点插入,导致二叉树不平衡

      • 如何旋转: 直接对整体进行右旋即可

        08_平衡二叉树左左

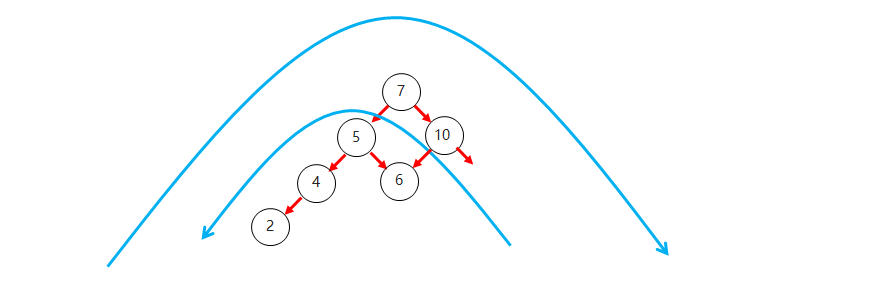
    • 左右

      • 左右: 当根节点左子树的右子树有节点插入,导致二叉树不平衡

      • 如何旋转: 先在左子树对应的节点位置进行左旋,在对整体进行右旋

        09_平衡二叉树左右

    • 右右

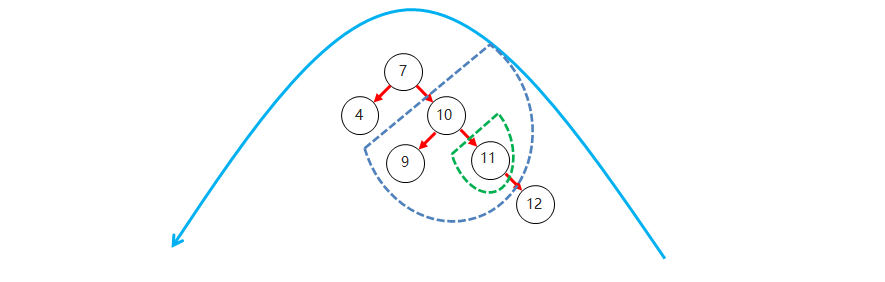
      • 右右: 当根节点右子树的右子树有节点插入,导致二叉树不平衡

      • 如何旋转: 直接对整体进行左旋即可

        10_平衡二叉树右右

    • 右左

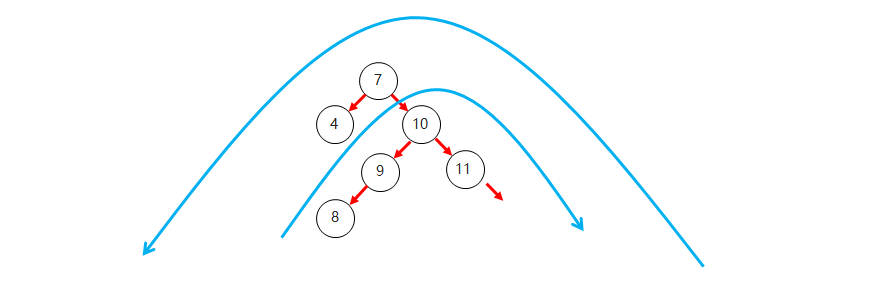
      • 右左:当根节点右子树的左子树有节点插入,导致二叉树不平衡

      • 如何旋转: 先在右子树对应的节点位置进行右旋,在对整体进行左旋

        11_平衡二叉树右左

*3.4 红黑树

  • 红黑树的特点

    • 平衡二叉B树；
    • 每一个节点可以是红或者黑；
    • 红黑树不是高度平衡的,它的平衡是通过"自己的红黑规则"进行实现的。

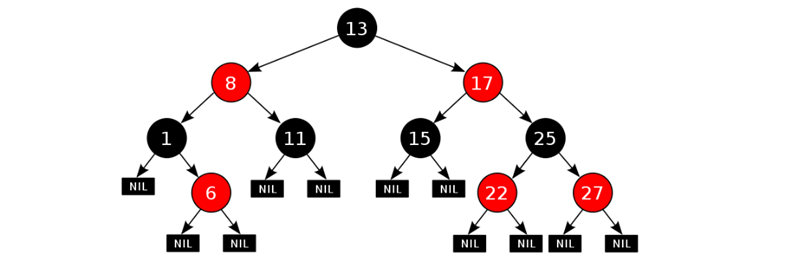
  • 红黑树的红黑规则有哪些

    1. 每一个节点或是红色的,或者是黑色的；

    2. 根节点必须是黑色；

    3. 如果一个节点没有子节点或者父节点,则该节点相应的指针属性值为Nil,这些Nil视为叶节点,每个叶节点(Nil)是黑色的；

    4. 如果某一个节点是红色,那么它的子节点必须是黑色(不能出现两个红色节点相连的情况)；

    5. 对每一个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点。

      12_红黑树结构图

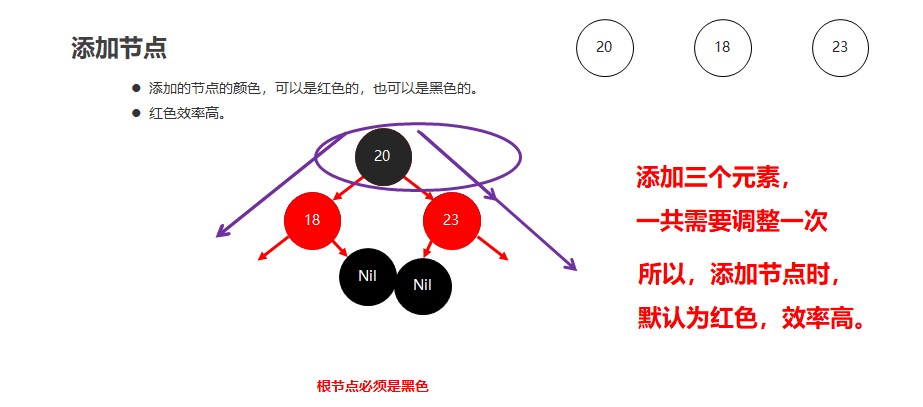
  • 红黑树添加节点的默认颜色

    • 添加节点时,默认为红色,效率高。

      13_红黑树添加节点颜色

  • 红黑树添加节点后如何保持红黑规则

    • 根节点位置
      • 直接变为黑色
    • 非根节点位置
      • 父节点为黑色
        • 不需要任何操作,默认红色即可
      • 父节点为红色
        • 叔叔节点为红色
          1. 将"父节点"设为黑色,将"叔叔节点"设为黑色
          2. 将"祖父节点"设为红色
          3. 如果"祖父节点"为根节点,则将根节点再次变成黑色
        • 叔叔节点为黑色
          1. 将"父节点"设为黑色
          2. 将"祖父节点"设为红色
          3. 以"祖父节点"为支点进行旋转
每日反思 Java后端 > Java
#Java
2024.2.17 Java基础（泛型+Set+数据结构）
https://fulequn.github.io/2024/02/Article202402171/
作者
Fulequn
发布于
2024年2月17日
许可协议