多MEC服务器系统中联合资源分配的任务卸载方案

复现论文：

移动边缘计算中联合资源分配的卸载策略研究_李栋

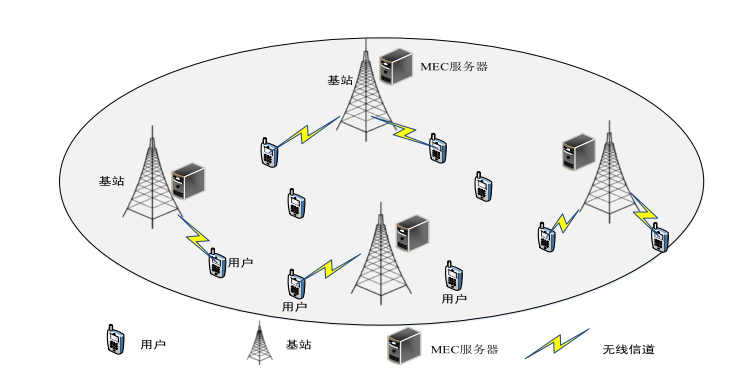
第4章 多MEC服务器系统中联合资源分配的任务卸载方案

1 系统模型及问题规划

该系统由多个用户和多个基站组成，每个基站上都部署有一个MEC服务器。在该系统中，假设有 I 个用户随机分布在整个网络中，所有用户的集合用 $I= \{ 1,2,\dots ,i, \dots ,I \}$ 表示，其中 I 表示为用户的数量。每个用户都有一个计算任务需要处理，用 $A_i=(d_i , c_i)$ 表示为第 i 个用户的计算任务，其中 $d_i$ 表示为计算任务的大小， $c_i$ 表示计算该任务所需的 CPU 周期数。把提供服务的基站和MEC服务器定义为服务节点，其集合表示为 $J = \{ 1,2,\dots ,i, \dots ,J \}$ ，其中 J 表示为服务节点的数量。每个服务节点都有有限的无线电资源和计算资源为用户提供服务。用 $\Phi_j = (W_j, C_j)$ 表示服务节点 j 的资源状态，其中 $W_j$ 表示为第 j 个服务节点拥有的无线电资源（表征为子信道数）， $C_j$ 表示为第 j 个服务节点拥有的单位计算资源的数量。

1.1 通信模型

使用 OFDMA作为上行链路传输机制，不考虑用户之间的干扰。当用户 i 选择将计算任务卸载到第 j 个 MEC 服务器执行时，其上行传输速率表示为

$$r_{i j}=w_{i j} \log _{2}\left(1+\frac{p_{i} h_{i j}}{\sigma_{i j}^{2}}\right)$$

$p_i$ 表示用户 i 的传输功率，$w_i$ 表示服务节点分配给 i 的信道带宽，$\sigma_{ij}^2$ 表示加性高斯白噪声功率，$h_{ij}$ 表示用户 i 与基站 j 之间的信道增益。

1.2 计算资源

1.本地计算时延和能耗

用户在本地处理任务的时间为

$$t_{il} = \frac{c_i}{f_i^l}$$

本地执行能耗为

$$e_{il} = \delta_i c_i$$

$f_i^l$ 表示用户 i 自身的计算能力，$\delta_i = 10^{-11} f_i^l$ 表示每个CPU周期消耗的能量。

2.远程计算时延和能耗模型

当用户i选择将任务卸载到 MEC 服务器 j 上执行的时候，用户终端会产生额外的时延成本，包括任务的传输时延、任务在MEC服务器进行处理的计算时延以及计算结果返回的时延。由于返回数据较小，忽略了结果返回的时延。用户i的任务卸载到服务节点 j 的时延表示为

$$t_{ij} = \frac{d_i}{r_{ij}} + \frac{c_i}{f_{ij}}$$

其中，$f_{ij}$ 表示为服务节点 j 分配给用户 i 的计算资源。

此时用户卸载消耗的能耗为任务传输的能耗，因此用户卸载能耗为

$$e_{ij} = p_i \frac{d_i}{r_{ij}}$$

这里只考虑每个用户卸载到一个服务器上的情况。对于任务是否卸载的问题，只需要满足计算卸载的任务运行时延和能耗不超过本地执行的时延能耗，即满足下面的表达式时可以进行卸载

$$t_{ij} \le t_{il} \\ e_{ij} \le e_{il}$$

用户选择卸载所需要的最小带宽为

$$w_{ij}^* = \frac{p_i d_i}{\delta_i c_i \log_2(1+p_i h_{ij} / \sigma_{ij}^2)}$$

因此，我们得到用户卸载所请求的子信道的数量

$$n_{ij} = \lceil w_{ij}^* / b \rceil$$

b 是子信道带宽。

用户选择卸载时服务节点 j 分配给用户i的最小计算资源为

$$f_{ij}^* = \frac{f_i^l c_i}{c_i - d_i f_i^l/w_{ij}^* \log_2(1+p_i h_{ij} / \sigma_{ij}^2) }$$

用户请求的单位计算资源数量为

$$m_{ij} = \lceil f_{ij}^* / g \rceil$$

g 表示计算资源的最小分配单位。

通信模型与计算模型主要是用来计算我们需要的资源的份数的。根据这两个模型来解释为什么用户需要这些固定份数的资源，之后的拍卖主要是用来解决服务器资源给谁的问题。这是两个部分，互不干扰。

1.3 计算费用模型

用户进行任务卸载时，应支付相应的报酬，以鼓励服务节点为其提供服务。用户i对服务节点 j 的资源竞标价格为

$$\rho_{ij} = \lambda_i^c m_{ij} + \lambda_i^w n_{ij}$$

$\lambda_i^c$ 表示为用户 i 的单位计算资源竞标价格，$\lambda_i^w$ 表示为用户 i 的单位无线电资源竞标价格。

服务节点 j 为用户 i 分配资源的成本为

$$\eta_{ij} = \beta_i^c m_{ij} + \beta_i^w n_{ij}$$

$\beta_i^c$ 表示服务节点 j 的单位计算资源成本，$\beta_i^w$ 表示服务节点 j 的单位无线电资源成本。

定义 $X= \{ x_{ij} \}_{I \times J}$ 为链接矩阵，其中 $x_{ij}$ 表示为链接变量，用户 i 与服务节点 j 建立链接的时候为1，不建立链接为0。服务节点 j 从用户 i 处得到的效益为

$$U_{ij} = x_{ij} (\rho_{ij} - \eta_{ij})$$

第 j 个服务节点整体效益可以表示为

$$U_j = \sum_{i=1}^I U_{ij}$$

1.4 优化问题

本文的目标是在满足服务节点资源限制的情况下最大化服务节点的效益，因此规划问题表示为

$$\begin{array}{l} \max \sum_{j=1}^{J} U_{j}=\sum_{j=1}^{J} \sum_{i=1}^{I} x_{i j}\left[\left(\lambda_{i}^{c}-\beta_{i}^{c}\right) m_{i j}+\left(\lambda_{i}^{w}-\beta_{i}^{w}\right) n_{i j}\right] \\ \text { s.t. } C1: \sum_{i=1}^{I} x_{i j} m_{i j} \leq C_{j}, \forall j \in J \\ \quad \quad C2: \sum_{i=1}^{I} x_{i j} n_{i j} \leq W_{j}, \forall j \in J \\ \quad \quad C3: \sum_{i=1}^{I} x_{i j} \leq 1, \forall j \in J \end{array}$$

其中，约束条件C1和 C2分别表示用户请求的计算资源和无线电资源不能超过服务节点的资源容量，约束C3表示一个用户最多由一个服务节点服务。

2 多轮组合拍卖算法

在本节中将式(4.16)表述的问题建模为组合拍卖模型，其中买家作为用户，卖家和拍卖商为拥有资源的服务节点，商品为服务节点拥有的无线电和计算资源。当用户需要卸载任务时，向周围的服务节点发送任务卸载和所需资源的请求信号，服务节点在接收到用户的请求信号后，向用户进行无线电及计算资源的拍卖。拍卖过程可以分为投标提交阶段以及获胜者确定阶段。

算法的主要步骤就是，m个用户，n个节点。每个用户都会对所有的节点进行打分，得到优先级。然后根据优先级决定自己要投标的节点。然后，每个节点会根据自己的投标信息执行赢家确定算法，使用动态规划的思路。我们可以得到最后的总收益、中标用户与未中标用户。最后，我们会更新未中标用户的出价，然后用户重新进行投标，直至现在不能够进行分配或者用户完全分配。

2.1 投标提交阶段

每个服务节点分别广播其可用的无线电资源 $W_j$，计算资源 $C_j$ 和其单位资源的成本。用户在接收到服务节点的信息后，考虑服务节点可用资源容量和服务节点到用户之间的距离作为评判因素。确定用户对于服务节点优先级序值，达到最优化选择。用户 i 对服务节点 j 的优先级 $o_{ij}$ 表示为

$$o_{ij} = \alpha \frac{W_j}{n_{ij}} + \beta \frac{C_j}{m_{ij}} + \gamma \frac{1}{l_{ij}}$$

其中，$\alpha$,$\beta$ ,$\gamma$分别是可用无线电资源因子、可用计算资源因子和距离因子，并且$\alpha + \beta + \gamma = 1$，$l_{ij}$ 表示用户 i 和服务节点 j 之间的距离。该式表明服务节点 j 可用资源越多并且和用户i距离越进，用户 i 对服务节点 j 的满意度就越高，更倾向于选择服务节点 j 进行任务的卸载。

用户在接收到服务节点的可用资源信息后，用户 i 根据优先级 $o_{ij}$ 对服务节点进行降序排序，排序集合表示为 $O_i^s$ ，然后用户根据排序集合中的元素，依次向其优先级最高的服务节点提交其出价的向量$(m_{ij}, n_{ij}, \lambda_i^c, \lambda_i^w)$，请求服务节点提供服务。

2.2 获胜者确定阶段

为了使得服务节点获得的效益最大化，服务节点可以抽象为一个背包，服务节点的计算资源和无线电资源的容量作为背包的容量。服务节点 j 在用户i处获得的效益 $U_{ij}$ 看作用户 i 所具有的价值，从而把服务节点资源分配问题抽象为一个二维背包问题，采用动态规划的方法来选择用户进行服务。其状态转移方程为

$$U_j(i, c, w) = \begin{cases} max \{ U_j(i-1, c, w), U_j(i-1, c-m_{ij},w-n_{ij})+U_{ij} \} \quad n_{ij} \le w \cup m_{ij} \le c \\ U_j(i-1,c,w) \quad \text{其他} \end{cases}$$

$U_j(i, c, w) $表示服务节点 j 在剩余无线电资源和计算资源容量分别 w 和 c 时选择前 i 个用户服务所获得的效益，$U_j(i-1, c, w)$ 表示前 i-1 个用户时服务节点 j 的收益，$U_j(i-1, c-m_{ij},w-n_{ij})+U_{ij}$ 表示的是服务节点 j 选择第 i 用户进行服务时获得的效益。

下面的是确定获胜者的算法。首先，判断用户 i 带来的价值是否能够满足个人理性，即节点选择为用户 i 服务能否得到收益。不带来收益的话，就可以直接宣布该用户未中标。在用户可以中标的前提下，我们使用动态规划的思想来判断选择哪些用户。判断的思路是，判断用户的资源需求是否可以被满足，如果可以被满足，我们就分两种情况进行考虑：1.服务节点 j 不选择为用户 i 服务，即 $U_j(i-1, c, w) > U_j(i-1, c-m_{ij}, w-n_{ij}) + U_{ij}$，节点收益为$U_j(i-1, c, w)$ ；2.服务节点 j 为用户 i 服务，用户的收益为$U_j(i-1, c-m_{ij}, w-n_{ij}) + U_{ij}$。若资源不足，则直接宣布用户未中标。

获胜者确定算法

输入：用户i的请求信息(m_i_j, n_i_j, lamb_i_c, lamb_i_w)，服务节点的资源容量{C_j, W_j}。
for 1:I_req_j do
	if U_i_j do
		for c=1:C_j do
			for w=1:W_j do
				if w_i <= w ∪ c_i <= c do
					if U_j(i-1, c, w) > U_j(i-1, c-m_i_j, w-n_i_j) + U_i_j do
						U_j(i, c, w) = U_j(i-1, c, w)
						x_ij = 0
						I_un = I_un ∪ {i}
					else
						x_ij = 1
						U_j(i, c, w) = U_j(i-1, c-m_i_j, w-n_i_j)+U_i_j
					end if
				else
					U_j(i, c, w) = U_j(i-1, c, w)
					x_i_j = 0
					I_un = I_un ∪ {i}
				end if
			end for
		end for
	else
		x_i_j = 0
		I_un = I_un ∪ {i}
	end if
end for
输出：服务节点效益U_j，未中标用户集合I_req_j，连接矩阵X。

下面的伪代码描述了多轮组合拍卖算法，其中一个服务节点表示为一轮决策，一共有 J 轮决策（具体的可以改变）。在每轮决策中，用户首先通过投标提交阶段确定自身对于服务节点的排序集合$O^s_i$，然后依次对$O^s_i$中的服务节点发送服务请求，提交其出价的向量。这个部分用户是只选择一个自己满意度最高的节点。服务节点在收到用户的请求后，会得到自己对应的申请用户列表。各节点会根据各自的用户申请，通过获胜者确定算法确定获胜的用户，并计算节点总效益。对于未能中标的用户将在下一轮中通过公式提高自身竞标价格并重新发送请求参与投标。

$$\lambda_i^c = \lambda_i^c + \Delta_i^c \lambda_i^c \\ \lambda_i^w = \lambda_i^w + \Delta_i^w \lambda_i^w$$

其中，$\Delta_i^c$和$\Delta_i^w$分别是无线电资源和计算资源单位价格的调整。

多轮组合拍卖算法

输入：用户的集合 I = {1,2,...,i,...,I}，服务节点集合 J={1,2,...,j,...,J}，用户的出价 (m_i_j, n_i_j, lam_c_i, lam_w_i)，服务节点的资源 {W_j, C_j},未中标集合I_un=I。
初始化： I_un=I
for R=1:J do
	for i=i:I_un do
        用户 i 根据式(4.17)计算对服务节点的优先级系数 o_ij，对优先级进行排序，确定排序集合 O_s_i，依次向 O_s_i 中的服务节点发送出价请求。
	for j=1:J do
		服务节点 j 接收到用户的请求信息后得到请求矩阵 I_req_j
		根据算法 4.1，得到服务节点效益 U_j，未中标用户集合 I_un 和连接矩阵 X。
		U_M=sum(U_j)
	end for
	更新未中标集合 I_un
	for i=1:I_un do
		根据式(4.19)和(4.20)更新其出价。
	end for
end for
输出：连接矩阵 X，效益 U_M ，未投标矩阵 I_un。

2.3 符号与一些问题

下面这些是在编程实现遇到的一些问题

1.符号方面

P_i 用户的传输功率

f_l_i 用户自身的计算能力

delta_i = 1e-11 f_l_i 表示为每个CPU周期消耗的能量

用 A_i = (d_i, c_i)表示为第i个用户的计算任务，其中d_i表示为计算任务的大小，c_i表示计算该任务所需的 CPU 周期数。

2.单位

注意dBm

功率的单位是瓦特（W），但是对于大多数实际应用来说，瓦特这个单位太大了。因此，在电信和信号处理领域，我们通常使用分贝（dB）来表示功率，这是一个对于非常大或非常小的值更易于管理的对数单位。

特别地，dBm单位通常用于表示电信信号的功率。它被定义为测量功率与1毫瓦（mW）参考功率的分贝（dB）功率比。因此，0 dBm代表1毫瓦的功率，而x dBm的功率水平表示10^(x/10) 毫瓦的功率。

因此，要从dBm转换为毫瓦，我们使用以下公式：
功率（mW）= 10^(功率（dBm）/10)

在给定的值-100 dBm和-80 dBm的情况下，它们代表非常低的功率水平。要将这些值转换为毫瓦，我们可以使用上述公式。对于-100 dBm，我们有：
功率（mW）= 10^（-100/10）= 10^（-10）= 0.0000000001 = 10^(-13)

类似地，对于-80 dBm，我们有：
功率（mW）= 10^（-80/10）= 10^（-8）= 0.00000001 = 10^(-11)

因此，-100 dBm用10^(-13)表示，-80 dBm用10^(-11)表示，是因为这些值对应于所描述的噪声信号的功率水平，并且它们已经使用上述公式转换为相应的毫瓦值。

GHz

还有GHz这个单位，f_ue = 6e8 # UE的计算频率0.6GHz

2.4 编程实现

# encoding: utf-8
"""
@version: python3.9
@author: ‘admin‘
@contact: 2382019442@qq.com
@software: PyCharm
@file: run_this.py
@time: 2023/6/11 15:37
"""
import math
import random
import numpy as np
import copy

random.seed(22)


class Link:

    def __init__(self, i, j):
        """
        建立用户i与节点j的通信链路，返回其他公式所需要的信息
        :param i: 用户
        :param j: 计算节点
        :return: 用于其他公式计算的信息
        """
        self.i = i
        self.j = j
        self.sigma_i_j2 = 1e-13  # 背景噪声 -100dBm
        # 两者之间距离
        self.l_i_j = (abs(i.location[0] - j.location[0]) ** 2 + abs(i.location[1] - j.location[1]) ** 2) ** 0.5
        self.h_i_j = self.l_i_j ** -4  # 链路的信道增益, 4是路径损耗指数
        # 任务卸载所需要的最小带宽
        self.w_i_j = 1e9 * i.P * i.d / (i.delta * i.c * math.log2(1 + i.P * self.h_i_j / self.sigma_i_j2))
        self.b = 5e6  # 子信道带宽 5MHz
        self.n_i_j = math.ceil(self.w_i_j / self.b)  # 所需最小子信道数目
        self.g = 2e9  # 计算资源最小分配单位 2GHz
        # 节点j分配给用户i的最小计算资源
        self.f_i_j = i.f_l * i.c / (i.c - i.d * i.f_l / self.w_i_j * math.log2(1 + i.P * self.h_i_j / self.sigma_i_j2))
        self.m_i_j = math.ceil(self.f_i_j / self.g * 100)  # 请求单位计算资源数量

        # 生成测试数据
        self.m_i_j = random.randint(12, 18)
        self.n_i_j = random.randint(12, 18)

        self.o_i_j = self.calculate_priority_coefficient()  # 用户对服务节点的优先级系数
        # 4.2.3 计算费用部分
        # 用户i对服务节点j的资源竞标价格
        self.rho_i_j = self.i.lamb_c * self.m_i_j + self.i.lamb_w * self.n_i_j
        # 服务节点j为用户i分配资源的成本
        self.eta_i_j = self.j.beta_c * self.m_i_j + self.j.beta_w * self.n_i_j
        self.x_i_j = 0  # 默认不建立链接

    def calculate_priority_coefficient(self):
        alpha = 0.3  # 可用无线电资源因子
        beta = 0.3  # 可用计算资源因子
        gamma = 0.4  # 距离因子
        if alpha + beta + gamma != 1:
            raise Exception("不满足 alpha+beta+gamma = 1 的前置要求")
        l = (abs(self.i.location[0] - self.j.location[0]) ** 2 + abs(
            self.i.location[1] - self.j.location[1]) ** 2) ** 0.5
        # 根据式(4.17)计算优先级系数
        o_i_j = alpha * self.j.w / self.n_i_j + beta * self.j.c / self.m_i_j + gamma * 1 / l
        return o_i_j

    # 计算用户i对节点j的价值
    def calculate_u_i_j(self):
        return self.x_i_j * (self.rho_i_j - self.eta_i_j)


def algorithm_4_1(I_req_j, X):
    """
    根据算法 4.1，得到服务节点效益 U_j，未中标用户集合 I_un 和连接矩阵 X
    :param I_req_j: list<Link> 所有向节点j请求的用户i建立的链路
    :return: 价值矩阵U_j, 分配结果X_list[0][req.j.c][req.j.w]
    """
    i = 1  # 记录用户数
    # x_i_j表示用户i与节点j之间的链路状态，如果建立链路则为1，否则为0。
    # 初始化U_j的二维数组
    # 在循环前初始化，防止每次新来一个都会刷新U_j
    U_j = np.array([[[0 for _ in range(I_req_j[0].j.w + 1)] \
                     for _ in range(I_req_j[0].j.c + 1)] for _ in range(len(I_req_j) + 1)])
    X_list = [[["" for _ in range(I_req_j[0].j.w + 1)] \
               for _ in range(I_req_j[0].j.c + 1)],
              [["" for _ in range(I_req_j[0].j.w + 1)] \
               for _ in range(I_req_j[0].j.c + 1)]
              ]
    for req in I_req_j:
        # 获取对应的序号
        i_id = req.i.id
        j_id = req.j.id
        u_i_j = req.rho_i_j - req.eta_i_j
        print("u_i_j : " + str(u_i_j))
        # 用户出价是否大于成本
        if u_i_j > 0:
            for c in range(0, req.j.c + 1):
                for w in range(0, req.j.w + 1):
                    # 当第i个用户所需的资源不超过服务节点 j 剩余资源容量的条件下
                    if req.n_i_j <= w and req.m_i_j <= c:
                        if U_j[i - 1, c, w] > U_j[i - 1, c - req.m_i_j, w - req.n_i_j] + u_i_j:
                            U_j[i, c, w] = U_j[i - 1, c, w]
                            # 服务节点j不选择为第i个用户服务
                            # X[i_id][j_id] = 0  # 不建立链路
                            X_list[1][c][w] = X_list[0][c][w] + "0"
                            # X_list[c, w] = np.append(X_list[i - 1, c, w], 0)
                            # 添加语句有问题，不应该是每次都添加
                            # 最后输出的I_un的数值太大
                            # 当c和w同时为最大值的时候的收益，就是我们最终的收益，分配矩阵就是我们的矩阵
                            # if c == req.j.c and w == req.j.w:
                            #     # X[i_id][j_id] = 0  # 不建立链路
                            #     I_un.append(req.i)
                        else:
                            # X[i_id][j_id] = 1  # 建立链路
                            X_list[1][c][w] = X_list[0][c - req.m_i_j][w - req.n_i_j] + "1"
                            U_j[i, c, w] = U_j[i - 1, c - req.m_i_j, w - req.n_i_j] + u_i_j
                            # 添加在这个地方不对，后面的需求循环不到
                            # if c == req.j.c and w == req.j.w:
                            #     X[i_id][j_id] = 1  # 建立链路
                            #     req.j.c, req.j.w = c - req.m_i_j, w - req.n_i_j
                    else:
                        U_j[i, c, w] = U_j[i - 1, c, w]
                        X_list[1][c][w] = X_list[0][c][w] + "0"
                        X[i_id][j_id] = 0  # 不建立链路
                        # if c == req.j.c and w == req.j.w:
                        #     I_un.append(req.i)
            X_list[0] = copy.deepcopy(X_list[1])
        # 用户出价小于成本
        else:
            X[i_id][j_id] = 0  # 不建立链路
            # X_list[i, c, w] = X_list[i, c, w] + "0"
            # 把用户i放入未中标集合I_un中
            # I_un.append(req.i)
        # print("X : " + str(X_list[0][req.j.c][req.j.w]))
        # 这里必须实现i+1，因为要更新所有的链接矩阵
        # 必须在使用i操作完之后再进行i+1，防止越界错误
        i += 1
    return U_j[i-1, req.j.c, req.j.w], X_list[0][req.j.c][req.j.w]


# 用户类
class User:
    _id = 0

    def __init__(self):
        self.id = User._id  # 标识
        User._id += 1
        self.P = 100  # 用户的传输功率 20dBm
        self.f_l = random.uniform(0.1, 1) * 1e9  # 用户自身的计算能力 GHz
        self.delta = 1e-11 * self.f_l  # 每个CPU周期消耗的能量
        # 用  A_i = (d_i, c_i)表示为第i个用户的计算任务
        self.d = random.randint(10, 100) * 1024  # 计算任务的大小 10~100kB
        self.c = random.randint(100, 1000) * 1e6  # 计算该任务所需的 CPU 周期数 Megacycle
        # 计算费用 5~10
        self.lamb_c = random.randint(5, 10)  # 单位计算资源竞标价格
        self.lamb_w = random.randint(5, 10)  # 单位无线电资源竞标价格
        # 更新投标价格用
        self.Delta_c = 2
        self.Delta_w = 2
        self.location = (random.randint(0, 1000), random.randint(0, 1000))  # 位置

    def __lt__(self, other):
        # 比较逻辑，根据自己的需求进行实现
        # 返回True表示当前对象小于other对象，否则返回False
        return self.id < other.id


# 计算节点
class Node:
    _id = 0

    def __init__(self):
        self.id = Node._id  # 标识
        Node._id += 1
        self.w = random.randint(20, 40)  # 无线电资源
        self.c = random.randint(20, 40)  # 计算资源
        # 计算费用 2~8
        self.beta_c = random.randint(2, 8)  # 单位计算资源成本
        self.beta_w = random.randint(2, 8)  # 单位无线电资源成本
        self.location = (random.randint(0, 1000), random.randint(0, 1000))  # 位置

    def __lt__(self, other):
        # 比较逻辑，根据自己的需求进行实现
        # 返回True表示当前对象小于other对象，否则返回False
        return self.id < other.id


def multi_combinatorial_auction(I, J):
    """
    多轮组合拍卖算法
    :param I: 用户的集合 I = {1,2,...,i,...,I} User
    :param J: 服务节点集合 J={1,2,...,j,...,J}, Node
    :return:
    """
    I_un = I  # 未中标用户
    X = [[0] * len(J) for _ in range(len(I))]  # 记录用户与节点之间的链路状态
    U_M = 0  # 拍卖的总收益
    # 一个服务节点表示为一轮决策，一共有J轮决策
    for N in J:
        # 4.3.1 投标提交阶段
        O_s = {}  # 存储用户的投标情况
        # 用户i
        for i in I_un:
            O_s_i = []
            # 所有的节点j
            for j in J:
                link_i_j = Link(i, j)
                # 用户 i 根据式(4.17)计算对服务节点的优先级系数 o_i_j
                o_i_j = link_i_j.o_i_j
                O_s_i.append((o_i_j, link_i_j))  # 将 (o_i_j, link_i_j) 二元组添加到列表中
            # 对优先级进行排序，确定排序集合 O_s_i，依次向 O_s_i 中的服务节点发送出价请求
            O_s_i = sorted(O_s_i, key=lambda x: x[0], reverse=True)  # 按照优先级系数进行降序排列

            # 记录成功报价
            j_id = O_s_i[0][1].j.id
            # 检查节点是否已经在字典中，如果不在则添加到字典中
            if j_id not in O_s:
                O_s[j_id] = []
            # 将用户列表添加到对应的节点键中
            O_s[j_id].append(O_s_i[0][1])
        # 用户根据排序集合中的元素，依次向其优先级最高的服务节点提交其出价的向量
        # 请求服务节点提供服务

        # 4.3.2 获胜者确定阶段
        # 记录每一轮所有未中标用户
        I_temp = []
        for j in J:
            # 服务节点 j 接收到用户的请求信息后得到请求列表 I_req_j
            j_id = j.id
            I_req_j = np.array(O_s.get(j_id, None))

            if None in I_req_j:
                continue

            # 根据算法 4.1，得到服务节点效益 U_j，未中标用户集合 I_un 和连接矩阵 X
            U_j_fin, X_final = algorithm_4_1(I_req_j, X)
            for i in range(len(X_final)):
                # 找到被分配的对象，然后削减资源
                if X_final[i] == "1":
                    j.c = j.c - I_req_j[i].m_i_j  # 分配计算资源
                    j.w = j.w - I_req_j[i].n_i_j  # 分配通信资源
                    X[i][j_id] = 1
                else:
                    I_temp = np.append(I_temp, I_req_j[i].i)
                    X[i][j_id] = 0
            U_M = U_M + U_j_fin

            # 更新未中标集合 I_un
            # I_un = np.concatenate((I_un, I_un_j), axis=0)
            # I_un = np.unique(I_un)

        # 更新I_un
        I_un = I_temp
        # 如果没有未中标的用户，提前跳出拍卖
        if not any(I_un):
            return X, U_M, I_un
        # 存在未中标用户，更新未中标用户的报价
        else:
            for i in I_un:
                # 根据式(4.19)和(4.20)更新其出价
                # 这里的更新方式带来的后果就是用户的出价过高，后面的收益太大
                i.lamb_c += i.lamb_c + i.Delta_c * i.lamb_c
                i.lamb_w += i.lamb_w + i.Delta_w * i.lamb_w
    # U_M是最后的总收益
    return X, U_M, I_un


if __name__ == "__main__":
    I = []
    J = []
    n1 = Node()
    n2 = Node()
    u1 = User()
    u2 = User()
    u3 = User()
    u4 = User()
    I.append(u1)
    I.append(u2)
    I.append(u3)
    I.append(u4)
    J.append(n1)
    J.append(n2)
    I = np.array(I)
    J = np.array(J)
    X, U_M, I_un = multi_combinatorial_auction(I, J)
    print("多轮组合拍卖的结果")
    print("X : " + str(X))
    print("U_M : " + str(U_M))
    print("I_un : " + str(I_un))

结果展示

u_i_j : 47
u_i_j : 33
u_i_j : 8
u_i_j : 63
u_i_j : 660
u_i_j : 690
u_i_j : 622
多轮组合拍卖的结果
X : [[0, 0], [1, 0], [0, 0], [0, 1]]
U_M : 753
I_un : [<__main__.User object at 0x0000017450F3C190>
 <__main__.User object at 0x0000017450F2EF70>]

3 改进的部分

3.1 用户定价与系统成本

3.2 通信和计算模型

3.3 求解方法 动态规划 强化学习