人工智能和计算机视觉(6)-二维几何变换

图像转换

图像转换无处不在。例如，模板匹配，形状匹配，图像搜索。图像转换是为了执行图像旋转，调整图像的位置或移动图像。

图像平移(translation)是用来将图像移动到一个新的位置。

旋转(Rotation)用于将图像按某一方向旋转，如顺时针或逆时针某种程度的旋转。

缩放(Scaling)或聚焦(zooming)是用来放大或缩小图像，需要指定要放大或缩小的图像的数量。

剪切(Shearing)是用来将图像扭曲成一个不同的形状或方向，围绕X或Y轴。

平移

图像的位置沿x轴（Tx）或y轴（Ty）移动。

当原坐标被指定为（x,y），而新的坐标是（x’，y’），其公式如下：

$$x^{'}=x+T_x \\ y^{'}=y+T_y$$

如果我们用一个矩阵来表示平移 P’=P+T，那么我们就有：

P^{'}=\left[ \matrix{ x^{'}\\ y^{'} } \right] \quad P=\left[ \matrix{ x\\ y } \right] \quad T=\left[ \matrix{ T_x\\ T_y } \right]

旋转

以(0,0)为原点，(x, y)可以用距离r和角度$\phi$来表示。

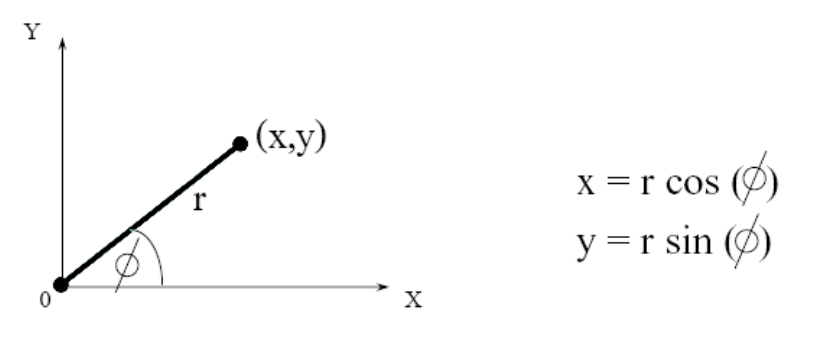
同理，新位置(x’,y’)也可以可以用距离r和角度$\phi$来表示。

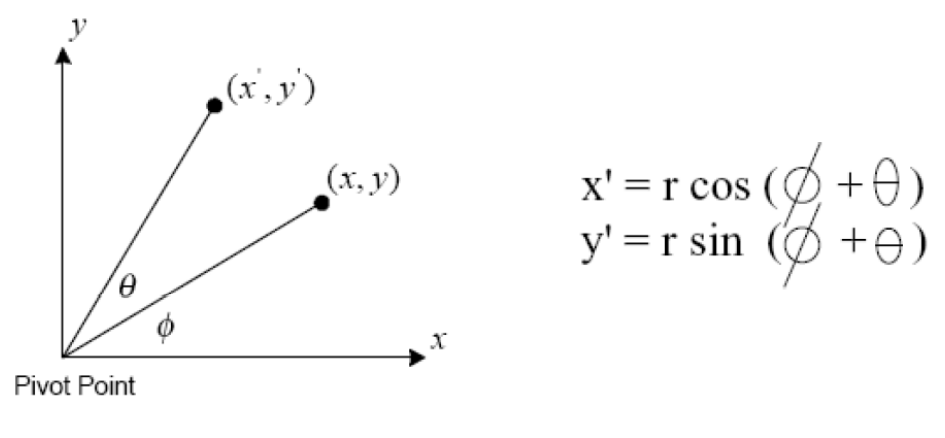
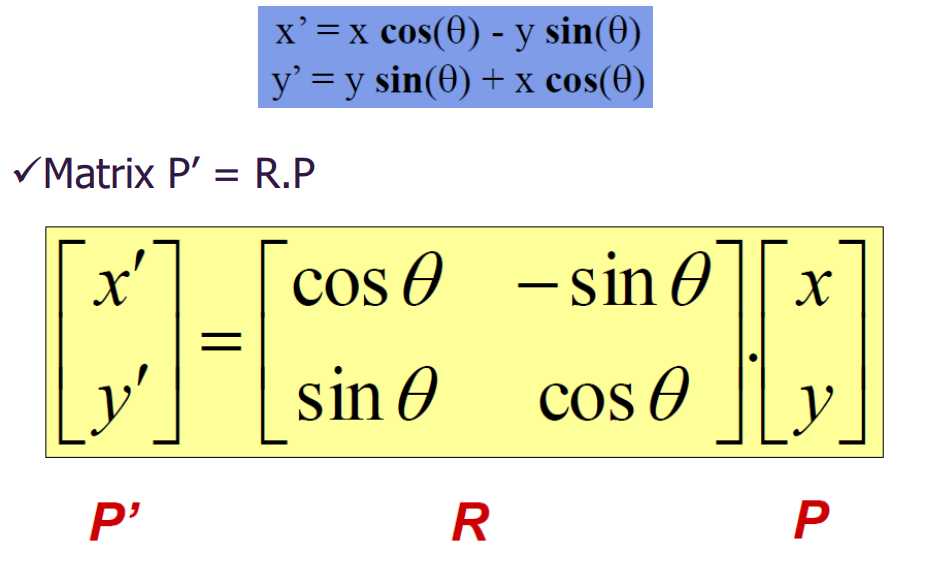
在原点以外的任何一点旋转图像都需要3个步骤。

1.将旋转点(xp, yp)移动到(0, 0)，并且移动（x，y）到一个新的点（x’，y’）。

2.围绕原点进行旋转。

3.通过添加xp和yp移动到同一点。

围绕任何不是原点的支点进行旋转。

$$x^{'}=[(x-xp)cos\theta -(y-yp)sin\theta]+xp \\ y^{'}=[(y-yp)sin\theta +(x-xp)cos\theta]+yp$$

缩放

缩放和放大图像可以通过以下方式进行使用缩放系数，包括Sx和Sy。用于放大和缩小图像分别用于沿x轴和y轴放大和缩小图像。

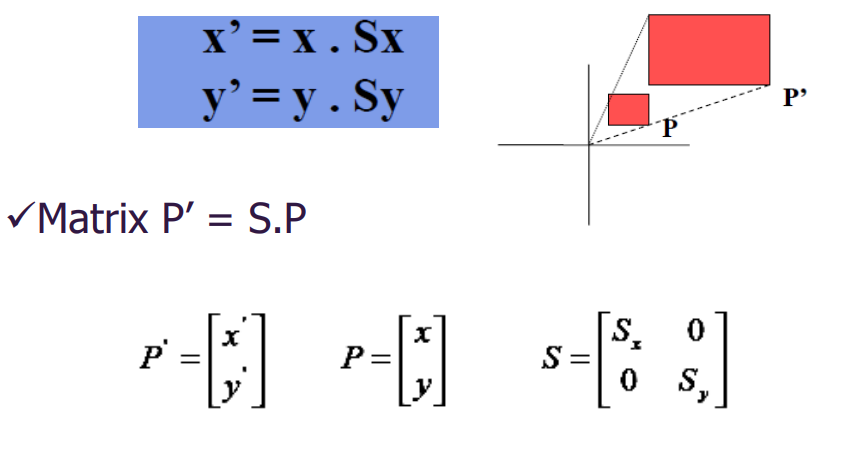
当固定点不在原点时，缩小和放大图像。

1.移动位置到原点。

2.围绕原点缩小或扩大。

3.移动到相同的固定点，具体如下:

$$x^{'}=(x-x_f)\cdot S_x + x_f \\ y^{'}=(y-y_f)\cdot S_y + y_f$$

缩放使用以下矩阵：

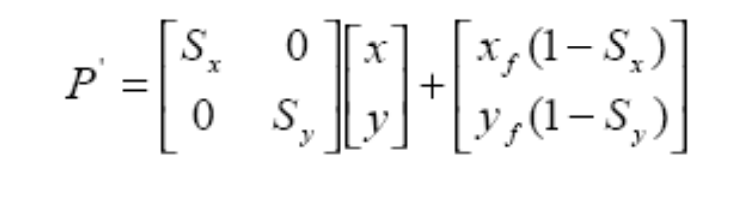
剪切

要调整图像扭曲的方向，包括x轴和y轴。

参考有两个位置：X和Y。这被称为笛卡尔坐标。它的缺点是，当转换多个时，图像转换矩阵的结果转换矩阵的结果将是加法的形式和乘法的矩阵。

齐次坐标系

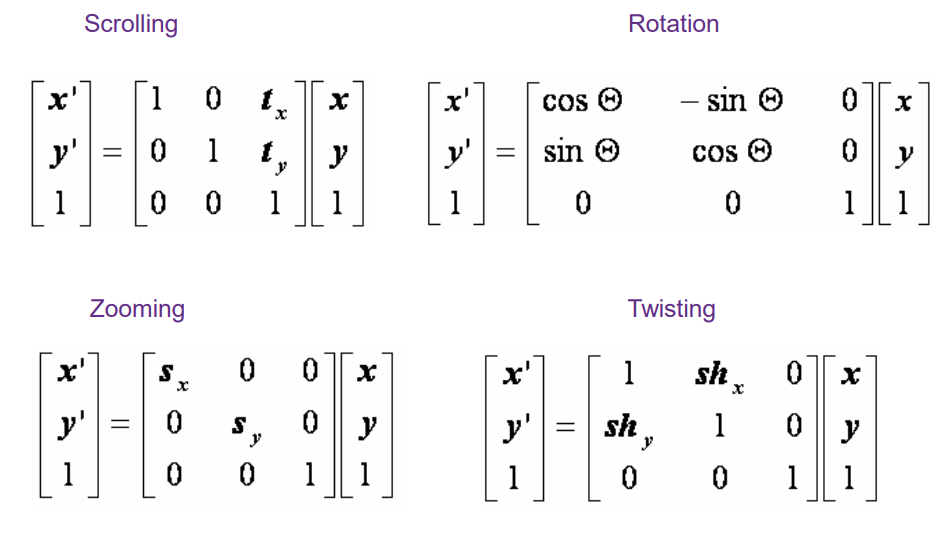
参考链接：

Apply 2-D spatial transformation to image - MATLAB imtransform - MathWorks United Kingdom