多无人机辅助移动边缘计算的高效卸载和轨迹调度

摘要:移动边缘计算 (MEC) 和无人机 (UAV) 的出现对物联网 (IoT) 的未来发展具有重要意义。额外的计算能力和广泛的网络覆盖为能源有限的智能移动设备 (SMDs) 提供了更多的机会来体验不同的智能应用。本文提出了多无人机辅助 MEC 系统的计算效率最大化问题，同时考虑了计算量和能量消耗。基于部分计算卸载模式，联合优化无人机用户关联、 CPU 周期频率、功率和频谱资源分配以及轨迹调度。由于问题的非凸性和变量间的耦合性，我们提出了一种双环结构的迭代优化算法来寻找最优解。仿真结果表明，该算法在保证计算服务质量的前提下，能够获得比基线方案更高的计算效率。

1.介绍

移动无线通信网络和物联网 (IoT) 的广泛发展，推动了智能移动设备 (SMD) 的空前普及，这为许多新颖的智能应用提供了强大的平台。这些应用，例如人脸识别、互动游戏和自动导航，通常需要密集的计算和带来更多的能源消耗。然而，由于 SMD 的计算资源和电池预算有限，导致了计算密集型应用与有限资源之间的冲突。移动边缘计算 (MEC) 是一种很有前途的方法，它允许 SMD 将其计算密集型的任务转移到边缘服务器，以解决冲突。边缘服务器部署在无线接入网络的边缘，接近 SMD。具体而言，与基于基础设施的蜂窝无线网络 MEC 部署相比，无人机辅助的 MEC 可以支持更灵活的移动计算业务。

无人机辅助的 MEC 系统可以被集成以提供广泛的覆盖和额外的计算能力，特别是对于那些基础设施有限或没有可用基础设施的无线系统，这已经受到越来越多的欢迎。例如，可以部署具有云服务器的无人机，以协助实现应急响应、网络威胁检测和自适应建议。文献 [9]和[10] 研究了无人机的高效部署和机动性，无人机被用作空中基站，通过地面物联网设备上行链路收集数据和计算任务。在文献 [11]中提出了三层无人机边缘云计算体系结构，研究了联合计算卸载和路由优化问题。由于有限的能量是无人机辅助MEC系统设计的主要问题，文献 [12]和[13] 分别侧重于节能资源分配和计算卸载问题。此外，文献 [14]和[15] 在无人机辅助的无线网络中应用博弈论来扩展通信容量，最小化网络开销。然而，由于无人机辅助 MEC 系统具有机动性和能量有限的特点，在满足严格的多目标要求方面仍存在许多挑战，如高计算位和低能耗。

为了提供计算或节能的移动服务，在无人机辅助的 MEC 网络中，更多的努力致力于共同优化资源分配和轨迹调度。文献 [18] 研究了一种基于无人机云的节能移动云计算体系结构，该体系结构综合考虑了位分配和无人机轨迹。针对离散二值模型、有限能量和无人机轨迹设计的约束条件，文献 [10] 中以最小化所有用户的最大时延之和为目标。在文献 [19] 中，考虑了部分计算卸载、社会内容缓存和无线电资源调度等约束条件，提出了一种基于能量感知的社交车联网无人机辅助MEC动态资源分配问题。文献 [20] 研究了无人机无线供电 MEC 网络中联合优化计算卸载和轨迹设计的计算速率最大化问题。在前期工作文献 [21] 中，提出了无人机辅助 MEC 系统中以 SMD和无人机加权平均能耗最小为目标的随机计算卸载、资源分配和轨迹调度联合优化问题。但由于上述工作仅采用了一架无人机来辅助 MEC 的实施，导致网络的可扩展性存在一定的不足。此外，为了扩大网络覆盖范围和服务更多的 SMD，可以使用多个无人机，其中用户关联是一个关键问题，尚未探索。在文献 [22] 中，提出了一种针对挑战网络的多无人机辅助 MEC 基础设施。虽然该系统专注于优化无人机的部署和用户关联，但资源分配和轨迹调度尚未得到解决。在文献 [23] 中提出了一种基于无人机的分层雾云计算系统，该系统综合考虑了计算卸载、用户云/云关联、发射功率分配和路径规划等问题，建立了加权总功耗最小问题。然而，在现有的工作中，对无人机辅助 MEC 系统中计算量和能耗的联合优化问题的研究还不够深入。

近年来，计算效率作为一种新的度量指标在蜂窝 MEC 网络在文献[24]，[25]中被提出。在文献[25]中，提出了无线供电 MEC 网络中公平性计算效率最大化问题，文献[26]的目标是使 SMD 计算效率的加权和最大化。计算效率不同于对延迟、能量和计算速率进行单独优化，计算效率是同时衡量 MEC 系统的计算位和能量消耗。因此，为了研究多无人机辅助 MEC 系统的计算效率最大化问题，本文主要研究无人机的用户关联、计算和通信资源分配以及轨迹调度的联合优化问题。本文的主要贡献如下:

• 我们考虑了一种计算效率高的多无人机辅助 MEC 系统，在该系统中，无人机被赋予计算服务器，以支持对处理能力有限的 SMD 的部分计算卸载。
• 通过计算效率来衡量系统的计算量和能耗。在多无人机辅助的 MEC 系统中，通过共同考虑用户关联、 CPU 周期频率分配、该问题为不同变量非线性耦合的非凸问题。
• 针对目标函数的分式结构，将该问题重构为参数规划问题，并提出了一种双环结构的迭代搜索算法来求解该问题。通过建立外环，利用 Dinkelbach 方法对计算效率进行求解和更新。在内环中提出了用户关联、资源分配和轨迹调度的联合优化算法。

本文的其余部分组织如下。第二部分介绍了系统模型和问题表述。在第三节中，为了使计算效率最大化，提出了一种双环结构的高效迭代搜索算法。第四节讨论了仿真结果。最后，我们在第五节总结了本文。

2.系统模型及问题公式

A.系统模型

如图 1 所示，考虑一种多无人机辅助 MEC 系统，该系统由 F 个无人机和 M 个地面 SMD 组成，表示为 $\mathcal{F} \triangleq\{1,2, \ldots, F\}$ 和 $\mathcal{M} \triangleq\{1,2, \ldots, M\}$ 。配备 MEC 服务器的无人机具有强大的计算能力，在地面 SMD 上完成从初始位置飞到指定最终位置的任务。 SMD 用于从环境中收集数据。由于计算资源有限， SMD 收集的部分感知数据可以通过无线链路传输到无人机上执行。该网络场景的实例可应用于智能集中充电、环境监测、协同作战等领域。该系统在指定的任务期间运行。为了便于展示，任务周期被划分为 N 个时隙，时隙长度为 $\tau$ ， $N \in \mathcal{T} \triangleq\{1,2, \ldots, N\}$。当时隙长度 $\tau = T/ N$ 足够小时，无人机可以飞行较短的距离，并在每个时隙内近似采样信道增益。在每个时隙期间，我们假设每架无人机都为其相关的地面 SMD 提供一个频分多址(FDMA)协议。

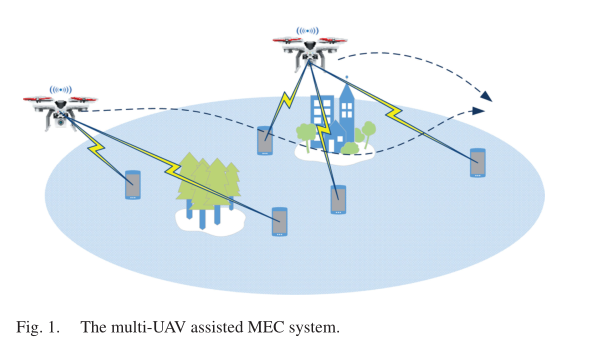
我们考虑一个三维(3D)笛卡尔坐标系，其中每个 SMD i∈M 分散在地面上，其水平坐标为 $u_i = (x_i, y_i)$ 。我们假定飞机在离地面高度 h 不变的情况下飞行。无人机 j 在时刻 n 投影到水平面上的飞行轨迹可以表示为 $q_j(n) = (x_j(n)， y_j(n))$ 。进而确定各障碍物中心在 MEC 网络中的水平坐标为 $b_m = (x_m, y_m)$ 。根据欧几里德公式，我们可以得到无人机 j 与 SMD i 在时间槽 n 处的距离为

$$d_{i, j}(n)=\sqrt{h^{2}+\left\|\mathbf{q}_{j}(n)-u_{i}\right\|^{2}}$$

一般来说，在 UAV-SMD 无线通信链路中，视距(LoS)信道比其他信道更占主导地位。与[10]和[18]相似，我们将 SMD i 和 UAV j 之间的无线信道视为自由空间路径损耗模型，可以表示为

$$h_{i, j}(n)=\beta_{0}\left(d_{i}(n)\right)^{-2}$$

式中 $\beta_{0}$ 表示参考距离 $d_0 = 1 m$ 处的信道功率增益。对于每个 SMD ，它的任务既可以在本地执行，也可以卸载到无人机上执行。我们引入一个二进制变量 $s_{i,j}(n)∈{0,1}$ 来区分不同的状态。 $s_{i,j}(n)=1$ 表示 SMD i 与无人机 j 在时刻 n 关联并服务，否则 $s_{i,j}(n)=0$ 。注意， $s_{i,j}(n)$ 不仅定义了计算卸载决策，还定义了每个时点的 UAV-SMD 关联。

1)本地计算

为了处理计算任务，每个 SMD 在不同的时隙具有有限的计算能力，记为 $f_i(n)$。令 ρ 为处理一个比特计算任务所需的 CPU 周期数。这样，在 SMD 上执行的计算位可以得到

$$R_{i}^{l}(n)=\frac{f_{i}(n) \tau}{\rho}$$

根据[20]， SMD i 用于局部计算的功耗被建模为 $p^l_i(n) = \kappa f_{i}^{3}(n)$ 。 $\kappa$ 为 CPU 的有效开关电容，其值取决于芯片的结构。因此， SMD i 在时间槽 n 处的局部能耗可以表示为

$$E_{i}^{l}(n)=\kappa f_{i}^{3}(n) \tau$$

2)无人机辅助边缘计算

当 SMD 选择将计算任务卸载给 MEC 服务器时，输入的数据需要通过无线上行链路传输给无人机。为了避免干扰和数据串扰，每个 SMD 在每个时隙只能关联一个无人机。另外，我们假设 SMD 到同一无人机上行链路的总频谱带宽为 W ，每个 SMD 可以使用不同的频谱资源访问无人机。设 $\alpha_{i,j}(n)$ 为分配给 SMD i， $\alpha_{i,j}(n)∈[0,1]$ 的频谱资源的比例。根据 Shannon-Hartley 公式[30]， SMD i 卸载到 UAV j 的计算位可以表示为

$$R_{i, j}^{c}(n)=\alpha_{i, j}(n) W \tau \log _{2}\left(1+\frac{p_{i, j}(n) h_{i, j}(n)}{\alpha_{i, j}(n) W N_{0}}\right)$$

式中 $p_{i, j}(n)$ 为 SMD i 的发射功率， $N_0$ 为噪声功率谱密度。传输卸载的计算位所消耗的相应能量由下式计算

$$E_{i, j}^{c}(n)=p_{i, j}(n) \tau$$

因此，在多无人机辅助的 MEC 网络中，总计算位由局部计算位和卸载位组成，计算结果为

$$R(X(n))=\sum_{n=1}^{N} \sum_{i=1}^{M}\left\{R_{i}^{l}(n)+\sum_{j=1}^{F} s_{i, j}(n) R_{i, j}^{c}(n)\right\}$$

式中， X(n) 为无人机用户关联、本地CPU运算周期频率、发射功率、频谱资源和飞行轨迹变量集，X(n) = {s(n)， f(n)， p(n)， α(n)， q(n)}。在系统总能耗方面，实际系统除传输和计算能耗外，还涉及到基带处理或备用电池[31]等静态能耗。与[25]类似，我们假设静态功率是一个恒定的 $P_c$ ，与其他能耗无关。那么，用于处理计算任务的 SMD 总能耗可表示为

$$E(X(n))=\sum_{n=1}^{N} \sum_{i=1}^{M}\left\{\kappa f_{i}^{3}(n)+\sum_{j=1}^{F} s_{i, j}(n) p_{i, j}(n)+P_{c}\right\} \tau$$

根据[26]，计算效率定义为总计算位数与总能耗的比值，有

$$\eta_{C E}=\frac{R(X(n))}{E(X(n))}$$

B.问题公式

本文重点研究了系统的计算效率最大化问题，同时对本地 cpu 周期频率、发射功率和频谱资源以及无人机飞行轨迹进行了联合优化。研究了部分计算卸载模式。因此，多无人机辅助 MEC 系统的计算效率最大化问题可以表述为

$$\begin{array}{ll} P: & \max _{\mathbf{X}(n)} \eta_{C E} \\ \text { s.t. } & C 1: 0 \leqslant f_{i}(n) \leqslant f_{i, \max }, \forall i, n, \\ & C 2: 0 \leqslant p_{i, j}(n) \leqslant p_{i, \max }, \forall i, j, n, \\ & C 3: \sum_{j=1}^{F} s_{i, j}(n) \leqslant 1, \forall i, n, \end{array}$$

$$\begin{array}{l} C 4: \sum_{i=1}^{M} s_{i, j}(n) \alpha_{i, j}(n) \leqslant 1, \forall j, n \\ C 5: \sum_{n=1}^{N}\left\{\frac{f_{i}(n) \tau}{\rho}+\sum_{j=1}^{F} s_{i, j}(n) \alpha_{i, j}(n) W \tau\right. \\ \left.\cdot \log _{2}\left(1+\frac{p_{i, j}(n) h_{i, j}(n)}{\alpha_{i, j}(n) W N_{0}}\right)\right\} \geqslant R_{\min }, \forall i \\ C 6:\left\|\mathbf{q}_{j}(n+1)-\mathbf{q}_{j}(n)\right\| \leqslant V_{\max } \tau, \forall j, n \\ C 7:\left\|\mathbf{q}_{j}(n)-\mathbf{q}_{l}(n)\right\| \geqslant d_{\min }, \forall n \in \mathcal{T}_{1}, l \neq j \\ C 8:\left\|\mathbf{q}_{j}(n)-\mathbf{b}_{m}\right\| \geqslant r_{m}, \forall j, n, m \\ C 9: \mathbf{q}_{j}(1)=\mathbf{q}_{I, j}, \mathbf{q}_{j}(N+1)=\mathbf{q}_{F, j}, \forall j \end{array}$$

在问题 P 中，C1 和 C2 给出了 SMD 的CPU-cycle frequency和发射功率的约束条件。C3表示每个SMD最多只能关联一个无人机。C4 是与相同无人机相关联的 SMD 的频谱资源分配约束。C5表示任务完成期间每个SMD的总计算位不能小于最小计算位，以保证计算服务质量(QoS)。C6为无人机最大飞行速度约束。C7和C8确保UA Vs之间以及UA Vs与障碍物之间的安全距离，以避免碰撞，其中T1 ={2，…， N}， rm为障碍物m的半径。I N C 9, qI,j, qF,j为UA V j的初始和最终位置。