物联网应用的空间/航空辅助计算卸载:一种基于学习的方法

摘要：物联网 (IoT) 计算卸载是一个具有挑战性的问题，特别是在公共边缘/云基础设施不可用的偏远地区。本文提出了一种空间-空-地综合网络 (SAGIN) 边缘/云计算体系结构，以减轻考虑远程能源和计算约束的计算密集型应用，其中飞行无人机提供近用户边缘计算，卫星提供云计算。首先，针对无人机边缘服务器，提出了一种联合资源分配和任务调度方法，有效地将计算资源分配给虚拟机，并对卸载后的任务进行调度。其次，我们研究了 SAGIN 中的计算卸载问题，提出了一种基于学习的方法，从动态 SAGIN 环境中学习最优的卸载策略。具体地说，我们将卸载决策过程表述为系统状态考虑网络动态的马尔可夫决策过程。针对系统的动态性和复杂性，提出了一种基于深度强化学习的计算卸载方法来实时学习最优卸载策略，其中采用策略梯度法处理较大的动作空间，并采用行为者批评法加速学习过程。仿真结果表明，所提出的边缘虚拟机分配和任务调度方法能够以极低的复杂度获得接近最优的性能，并且所提出的基于学习的计算卸载算法与其他卸载方法相比，不仅收敛速度快，而且总开销也较低。

1.介绍

随着 5G 网络和物联网的快速发展,出现了无数的有前途的应用程序和服务,如虚拟现实、高清直播、自主驾驶、工业自动化、智能家居等等,具有 5G 网络提供的好处,比如超高数据率,低延迟,高可靠性，海量连接。然而，除了高效可靠的通信外，广泛的应用也需要大量的计算能力。例如，虚拟现实和高清视屏需要大量的计算资源进行渲染和视频编码/解码，而自动驾驶汽车的转向控制则依赖于计算。这些计算密集型应用对资源受限的终端设备，特别是物联网设备的电池和计算能力提出了巨大的挑战，从而推动了云计算的发展。云计算将计算密集型应用卸载到云服务器上，云服务器具有集中而丰富的计算资源。尽管云计算可以大大降低计算延迟和能源消费的用户,它可能无法满足的要求延迟敏感的应用程序,如手机游戏和增强现实,因为长云终端用户和服务器之间传输的距离导致长传输延迟。为了解决这个问题，移动边缘计算(mobile edge computing, MEC)被广泛研究，它利用网络边缘的计算资源提供高效、灵活的计算服务。在 5G 无线系统中，将部署超密集的网络边缘设备，如宏/小蜂窝基站、 WiFi 接入点等，可提供指数级增长的边缘计算资源。 MEC 中的许多重要问题得到了广泛的研究，包括卸载任务模型、能量效率、时延减少、通信和计算的联合优化。

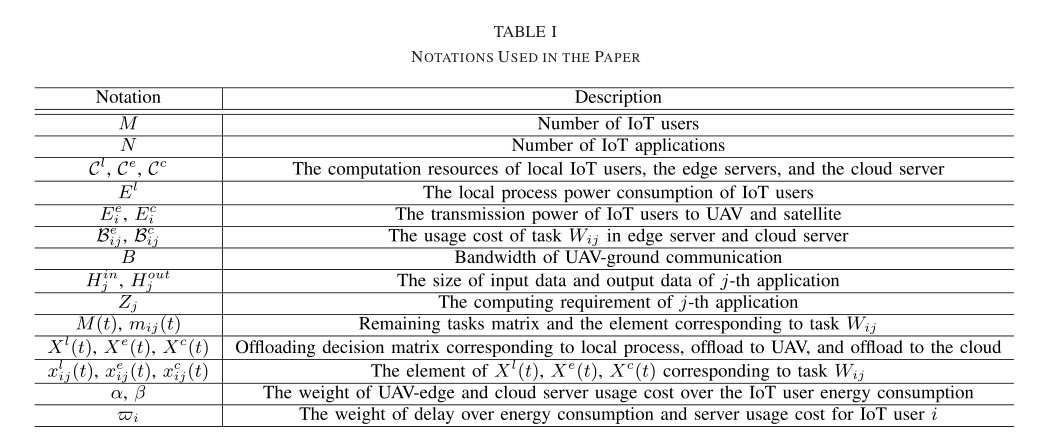
然而， 5G 网络可能无法在郊区和农村地区提供无所不在的覆盖，在这些地区，物联网设备可能会被广泛部署，以执行某些计算要求相对较高的应用程序。例如，传感信息的融合，特别是处理高清晰度的声音或视频信息，将迅速耗尽下沉节点的电池，导致巨大的处理延迟。由于缺乏地面接入网的覆盖，典型的边缘计算和云计算范式无法应用于这种场景。为此，我们建议采用 Space-Air-Ground 集成网络(SAGIN)架构，用于远程物联网应用的计算卸载。

SAGIN 将卫星网络、空中网络和地面网络相结合，为大范围提供无缝、灵活的网络覆盖和服务，可应用于智能交通系统、偏远地区监测、灾害救援、大规模高速移动互联网接入。 SAGIN 是由卫星网、空中网、地面网三个网段组成的多维异构网络。每个网段拥有不同的资源，受到不同的限制。低地球轨道 (LEO) 和地球静止轨道 (GEO) 卫星构成了一个层次网络，低地球轨道卫星提供高速访问，地球静止轨道卫星在低地球轨道之间中继数据进行长距离传输。空中网络包括飞行无人机、高纬度平台、通信气球等，可按需部署在数据流量突发的地点，提供动态覆盖、边缘计算、群体感知等高速、动态的网络服务。在提出的 SAG-IoT 计算卸载体系结构中，空中网络节点可以作为飞行边缘服务器，为物联网设备提供低延迟边缘计算。另一方面，卫星通信虽然可能具有较低的通信速率和较高的传输延迟，但可以通过无缝覆盖和卫星骨干网提供始终在线的云计算。然而，在物联网计算卸载中使用 SAGIN 引入了几个具有挑战性的问题。首先，由于空中网络的高移动性，信道条件和覆盖范围是动态的，导致服务器可用性和通信时延的变化，需要谨慎处理，以保证 SAG-IoT 系统的性能。其次， SAGIN 中不同网段具有不同的网络条件和资源约束，考虑复杂动态的网络条件和资源，设计一种高效的计算卸载方法是非简单的。

本文提出了一种灵活的联合通信和计算 SAGIN 框架，为远程物联网用户提供强大的边缘/云计算服务。在此框架下，我们提出了一种高效的计算卸载方法，该方法考虑多维网络动态和资源约束，实时学习最优卸载策略，使延迟、能量消耗和服务器使用成本加权和最小。首先，将无人机边缘服务器的计算资源虚拟化为虚拟机(VM)，并行执行卸载的任务;我们将联合虚拟机资源分配和任务调度问题表述为混合整数规划问题，并提出一种有效的启发式算法来求解。其次，我们研究了 SAGIN 中的计算卸载问题，将其表述为马尔可夫决策过程 (MDP) 。为了学习网络动力学，提出了一种基于无模型的强化学习方法，并设计了一种处理大状态和动作空间的 actor-critic 学习算法。据我们所知，我们的工作是研究 SAGIN 中计算卸载问题的第一个工作，这验证了 SAGIN 支持远程物联网用户计算密集型应用的可行性，并可以为 SAGIN 网络设计和远程计算卸载提供有用的指导。

本文的主要贡献可以总结如下:

• 我们将 SAG-IoT 计算卸载问题定义为 MDP ，并提出一种基于 RL 的方法来有效地解决该问题。定义系统状态，整合网络历史信息，学习系统动态。此外，提出了一种基于策略梯度的 actor-critic 学习算法，以解决维数诅咒问题，提高学习速度。
• 我们采用网络虚拟化，灵活分配边缘服务器的资源。将联合边缘服务器虚拟机计算资源分配和任务调度问题定义为混合整数规划问题，并提出了一种有效的启发式算法来求解。
• 通过大量的仿真来评估所提出方法的性能。联合虚拟机分配和任务调度能够以较低的复杂度达到接近最优的性能。此外，本文还就设计参数对所提出的基于 RL 的计算卸载方法的性能进行了评估。

本文的其余部分组织如下。在第二节中，我们介绍了相关的工作。第三部分描述了系统模型。第四节给出并解决了联合边缘虚拟机分配和任务调度问题。第五节阐述了 SAG-IoT 计算卸载问题，然后在第六节提出了基于 RL 的解决方案。第七节评估了所提出的方法，第八节总结了本文。表 1 列出了本文中使用的一些有用的符号。

2.相关工作

A.移动边缘计算

MEC 的概念最初由 ETSI 在文献 [18] 中提出，讨论了 MEC 的动机、定义、体系结构和具有挑战性的问题。在边缘计算中，计算任务的卸载机制决定了 MEC 系统的整体性能。节能计算卸载对于能量受限的物联网设备至关重要，在文献 [5]和[6] 中进行了研究。在文献 [5] 中， Mahmoodi 等人研究了联合调度和计算卸载问题，提出了一种基于真实数据测量的优化方法，以节省移动用户的能耗。在文献 [6] 中，Mao 等人提出了一种基于 Lyapunov 方法的能量收集设备动态计算卸载方法。同时考虑了执行延迟和任务失败的执行成本作为性能指标。在 MEC 系统中，能量消耗和任务延迟不仅依赖于任务的处理，还依赖于任务相关数据的通信。因此，通信无线电资源的联合优化与计算卸载问题引起了广泛的研究。在文献 [11] 中， You 等研究了 TDMA 和 OFDMA 场景下的多用户 MEC 卸载问题的资源分配问题。在文献 [12] 中， Wu 等人研究了多访问辅助计算卸载，提出了计算任务调度和无线电资源分配的联合优化。但这些工作只关注固定的 MEC 场景，即边缘计算服务由蜂窝 BSe 或 WiFi AP 提供，这与我们的工作中飞行无人机作为移动边缘服务器不同。在文献 [19] 中，提出了一种移动边缘计算机制。通过求解非凸优化问题，将钻头分配和无人机轨迹联合设计，使移动能耗最小。与文献 [19] 不同，我们同时考虑了能量消耗和任务处理延迟。此外，在无人机未被网络运营商部署且轨迹未知的情况下，无人机轨迹是学习而不是设计的。

B.Space-Air-Ground 集成网络

SAGIN 被认为是一种很有前途的技术，可以解决未来移动通信网络的许多问题，如远程和大规模覆盖、移动数据增长、数据流量不均衡、刚性骨干网等，近年来受到学术界和业界的广泛关注。在文献 [20]，[21] 中讨论了不同的 SAGIN 体系结构。在文献 [20] 中， Hoang 等人研究了 SAGIN 中的最优能量分配问题，提出了一种基于学习的算法来优化网络性能，使服务提供商的收益最大化。在文献 [21] 中， Zhang 等人提出了一个软件定义的 SAGIN 体系结构，并讨论了其中具有挑战性的问题。在 SAGIN 中采用了边缘缓存技术，减少了内容检索的延迟，减轻了骨干网的负担。在文献 [22] 中， Chen 等人考虑到用户信息和内容请求分布，提出了一种最优内容缓存方案，将内容放置在无人机中。然而，对于空间网段、航路网段、地面网段协同下的边缘计算卸载和计算资源分配的研究尚属空白，这对于支持 SAGIN 中大量计算密集型应用具有重要意义。

3.系统模型

A.网络模型

我们考虑了一个偏远地区，在那里部署物联网设备来执行某些具有计算需求的任务，如监控和视频监控。在考虑的偏远地区，没有蜂窝网络覆盖，因此我们考虑建立空-空-地综合网络 (SAGIN) ，为物联网设备提供网络接入、边缘计算和缓存等网络功能。图 1 为 SAG-IoT 组网概述。在 SAG-IoT 组网中，有地面网段、空中网段和空间网段。物联网设备组成地面部分，具有非常有限的能源和计算能力。在物联网设备上运行的应用程序可以生成要上传的数据和要执行的计算任务。在空中部分，飞行无人机可以作为边缘服务器，为地面用户提供边缘缓存和计算能力。像 Facebook Aquila 这样的飞行无人机，可以使用太阳能电池板在不充电的情况下飞行数月。无人机配置有固定的飞行轨迹来服务考虑的区域。此外，在空间段，一颗或多颗 LEO 卫星提供所关注区域的全覆盖，并通过卫星骨干网将物联网设备与云服务器连接起来。

对于物联网设备(用户) i ，它具有 $C^l$ 的本地计算能力，假设对所有用户都是相同的。局部任务计算/处理的能量消耗用 $E^l$ 表示，与 $C^l$ 有关。传输到无人机和卫星的功耗分别用 $E^e_i$ 和 $E^c_i$ 表示。在边缘服务器(即无人机)中，计算资源被虚拟化为虚拟机，每个虚拟机用于一个特定的应用程序[24]。在边缘服务器 k 中，总计算资源为 $C^e$ ，分配给计算虚拟机 v 的资源用 $C^e_v$ 表示，用户 i 的任务 j 的计算虚拟机使用服务器的代价用 $B^e_{i,j}$ 表示。对于无人机与地面的通信，由于考虑了任务卸载决策的时间尺度比传统的资源调度时间 (1 ms) 长得多，因此只考虑了大规模信道衰落。此外，由于不需要即时的信道信息，卫星控制的全球决策是可行的。根据[25]，得到无人机与地面用户之间的路径损失

$$\begin{array}{r} L(r, h)=20 \log \left(\frac{4 \pi f_{c}\left(h^{2}+r^{2}\right)^{\frac{1}{2}}}{c}\right)+P_{L o S}(r, h) \eta_{L o S} \\ +\left(1-P_{L o S}(r, h)\right) \eta_{N L o S} \end{array}$$

式中 h、r 分别为无人机的飞行高度和无人机到地面用户的水平距离。 $η_{LoS}$和 $\eta_{N L o S}$ 分别表示 LoS和NLoS 链[26]在自由空间路径损失上的附加损失。 $f_c$ 为载波频率， c 为光速。 $P_{LoS}$是无人机与地面链路的视距概率，可以通过

$$P_{L o S}(r, h)=\frac{1}{1+a \exp \left(-b\left(\arctan \left(\frac{h}{r}\right)-a\right)\right)}$$

$(a, b，η_{LoS}，η_{NLoS})$是环境因变量。例如，在偏远地区，它们的值为(4.88,0.43,0.1,21)[27]。此外，无人机与地面通信采用 WiFi 协议，总带宽为 b 。如果有 n 台物联网设备同时与无人机通信，则每台物联网设备获得的带宽为

$$B_i = \rho B \xi(n)$$

其中， ρ 为 WiFi 吞吐量效率因子， $\xi(n)$ 为 WiFi 信道利用率函数，该函数是满足用户数量 n 的递减函数。因此，即时无人机对地面和地面对无人机的数据速率表示为：

$$r_{G U}=\rho B \xi(n) \log _{2}\left(1+\frac{E_{i}^{e} 10^{-L_{i} / 10}}{\sigma^{2}}\right)$$

和

$$r_{UG}=\rho B \xi(n) \log _{2}\left(1+\frac{E_{i}^{e-} 10^{-L_{i} / 10}}{\sigma^{2}}\right)$$

式中， $E_{i}^{e-}$ 为无人机向地面物联网用户的发送功率， $L_i$ 为物联网用户-无人机链路的路径损耗， $σ^2$ 为高斯噪声功率。对于星地通信，我们考虑一个恒定的通信数据速率 $r_{SG}$ , 通常小于无人机对地数据速率。卫星通过卫星骨干网连接到互联网/云。我们用 $r_{SG}$ 表示卫星与云之间的传输速率。云的计算能力比物联网设备和边缘服务器高得多，每个任务的处理速率用 $C^c$ 表示，用户 i 的任务 j 的使用成本用 $B^c_{i,j}$ 表示。

B.多用户多任务 SAG-IoT 计算卸载

我们认为有 M 个物联网用户和 N 个不同的计算应用程序，每个用户运行所有 N 个应用程序，导致系统中有 M × N 个计算任务。同时考虑 N 个应用具有一定的优先级，即当同时调度多个任务时，应用数较小的任务会比应用数较大的任务先传输/处理。对于第 j 个应用程序，输入数据的大小、输出数据的大小、工作负载的大小分别用 $H^{in}_j$ 、 $H^{out}_j$ 、$Z_j$表示。这些任务可以在物联网设备上本地执行。然而，由于物联网设备的能源和计算能力有限，计算任务也可以通过无人机边缘服务器或进一步通过卫星转移到云。在每个时隙中做出卸载决策，直到所有 M × N 个任务全部完成。在 t 时段开始时，剩余任务用 M × N 矩阵 M(t) 表示，其中元素 $m_{i,j}(t) = 1$ 表示任务 $W_{ij}$ 未完成，否则 $m_{i,j}(t) = 0$ 。表示决定在本地处理任务,把任务边缘,并卸载任务云在时间 t 用 M×N 的矩阵 $X_l(t)$ , $X_e(t)$ 和 $X_c(t)$ 分别和每个二进制元素 $x^l_{ij}(t),x^e_{ij}(t),x^c_{ij}(t)$ 表明任务分别在本地处理,卸载到边缘或卸载到云。注意，任务 $W_{ij}$ 最多可以被调度到 t 时刻，卸载决策受限于

$$\begin{aligned} x_{i j}^{l}(t), x_{i j}^{e}(t), x_{i j}^{c}(t) & \in\{0,1\} \\ x_{i j}^{l}(t)+x_{i j}^{e}(t)+x_{i j}^{c}(t) & \leq m_{i j}(t) \end{aligned}$$

(7) 中的不等式在时间槽 t 没有调度未完成的任务时成立。如果任务 $W_{ij}$ 在 t 时刻被本地处理或卸载到云上，我们认为任务可以在一定的延迟下完成， $m_{i,j}(t+1) = 0$ 。但是，如果 $W_{ij}$被卸载到无人机边缘服务器，可能在 t 结束时无法完成并成功返回给用户 i ，这有两个原因。首先，如果将多个任务分配给一个无人机边缘服务器，其中一些任务可能无法在时间段内完成;其次，由于无人机是移动的，当任务 $W_{ij}$ 在边缘服务器中完成时，如果用户 i 在无人机的覆盖范围之外，则无法将结果传递给用户 i 。

C.成本模型

计算任务卸载是为了使执行 M × N 个任务的系统成本最小化。在考虑的 SAG-IoT 系统中，系统成本由延迟成本和能量及服务器使用成本两部分组成。

1)延迟成本:如果任务 $W_{ij}$ 被调度在时间间隔 t ，则根据卸载决策计算延迟。如果任务被安排在本地处理，则延迟为

$$T_{i j}^{l}=\varepsilon(t-1)+t_{r, i}^{l}+\frac{Z_{j}}{\mathcal{C}^{l}}$$

其中， ε 是时隙的长度，而 ε(t−1) 是自任务生成以来所经过的时间。由于物联网设备的计算能力较低，在 t 时段开始时，很可能有一些计划在本地处理的任务尚未完成。 $t^l_{r,i}$ 是用户 i 完成剩余本地处理任务的时间，可用剩余本地工作负载除以本地处理能力 $C^l$ 计算。如果将任务分配给无人机边缘服务器，在时间间隔 t 内将结果返回给用户 i ，则计算该任务的总延迟为

$$T_{i j}^{e}=\varepsilon(t-1)+d_{i j}^{e}+\frac{\sum_{a=1}^{j} x_{i, a}^{e}(t) H_{a}^{i n}}{r_{G U}}+\frac{H_{j}^{\text {out }}}{r_{U G}}$$

式中， $d_{i j}^{e}$ 为无人机边缘服务器中 $W_{ij}$ 的处理延迟，该延迟取决于第四节中服务器中的卸载决策和虚拟机资源分配。如果将用户 i 的多个任务调度到边缘服务器，考虑到有更高优先级的任务传输， $\sum_{a=1}^{j} x_{i, a}^{e}(t) H_{a}^{i n}$ 计算 $W_{ij}$ 任务数据传输到服务器的时间。类似地，如果任务通过卫星卸载到云上，则计算延迟为

$$T_{i j}^{c}=\varepsilon t+\frac{Z_{j}}{\mathcal{C}^{c}}+\frac{H_{j}^{i n}+H_{j}^{\text {out }}}{r_{S G}}+\frac{H_{j}^{i n}+H_{j}^{\text {out }}}{r_{S C}}$$

2)能量和服务器使用成本:本地处理 $W_{ij}$ 的能量成本可以通过下式计算：

$$L_{i j}^{l}=E^{l} \frac{Z_{j}}{\mathcal{C}^{l}}$$

如果在时间 t 时，任务 $W_{ij}$ 被分配给无人机边缘服务器，并成功传输给用户 i ，则计算出能量和服务器使用成本：

$$L_{i j}^{e}=E_{i}^{e} \sum_{t=1}^{v} x_{i j}^{e}(t) \frac{H_{j}^{i n}}{r_{G U}(t)}+\alpha \mathcal{B}_{i j}^{e}$$

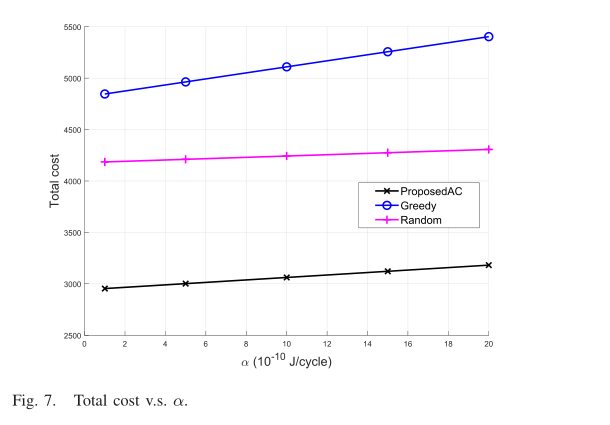
其中， α 表示无人机服务器使用成本相对于物联网用户能耗的权重。 $\sum_{t=1}^{v} x_{i j}^{e}(t) \frac{H_{j}^{i n}}{r_{G U}(t)}$ 计算总能耗，考虑到之前将任务卸给无人机边缘服务器的次数未能在调度槽内返回。类似地，如果任务 $W_{ij}$ 被卸载到云中，则可以计算出能量和服务器使用成本：

$$L_{i j}^{c}=\frac{E_{i}^{c} H_{j}^{i n}}{r_{S G}}+\beta \mathcal{B}_{i j}^{c}$$

式中β为云服务器使用成本对物联网用户能耗的权重。

4.计算虚拟机分配

在时间间隔 t 时，多个任务可以卸载到一个 UAV 边缘服务器上。在这种场景下，这些任务在不同的虚拟机中并行执行，以减少处理延迟。一个 VM 执行属于特定应用程序的任务。因此，我们研究了一个虚拟机分配问题，将边缘服务器的计算资源分配给不同的虚拟机，考虑到任务被分配到边缘服务器。此外，由于无人机的机动性，部分用户可能会在短时间内与无人机失去连接，在执行这些任务时，可能会导致分配给虚拟机的资源过多。例如,在图 2 中,两个虚拟机被认为是执行卸载任务无人机边缘服务器, $t_{i,j}$ 是 VM i 上任务 j的时延需求。我们可以看到延迟要求 $t_{2,1}$ 是非常严格和更大数量的计算资源应该分配给 VM2 期限前完成相应的任务。但是，由于边缘服务器的总计算资源是固定的，分配给 VM1 的资源很可能很少， VM1 中的三个任务都不能及时完成。因此，我们在无人机边缘服务器上联合优化虚拟机分配和任务调度，以减少系统总和延迟。

在所考虑的问题中，存在多种应用程序(Apps)，用A ={1，…，N}， 1台无人机边缘服务器，计算能力为 C 次循环每秒。对于第 m 个App，可能有多个卸载任务，用 $T_m ={1, \dots ,N_m}$ ，计算量相同，但最大延迟要求不同。注意， $Z_m$ 表示第 m 个应用程序的任务的计算工作量。 $C = {c_m | m \in A}$ 表示计算资源变量,其中 $c_m$ 是分配给虚拟机执行应用 m 的计算资源。 $Y = {y_{m,n} | m \in A,n \in T_m}$ 表示任务执行的决策变量, $y_{m,n}$ 的应用m n = 1如果任务是计划和执行,否则 $y_{m,n}=0$ 。因此，我们的和延迟最小化问题可以表示为:

$$\min _{\mathbf{C}, \mathbf{Y}} \sum_{m=1}^{N} \sum_{n=1}^{N_{m}}\left[y_{m, n} \sum_{k=1}^{n} y_{m, k} \frac{Z_{m}}{c_{m}}+\varepsilon\left(1-y_{m, n}\right)\right] \\ s.t. \mathrm{C} 1: \sum_{k=1}^{n} y_{m, k} \frac{Z_{m}}{c_{m}} \leqslant t_{m, n}, \quad \forall m \in \mathcal{A}, \forall n \in \mathcal{T}_{m} \\ \mathrm{C} 2: \sum_{m=1}^{M} c_{m} \leqslant \mathcal{C} \\ C3: c_{m} \geqslant 0 \\ \mathrm{C} 4: \quad y_{m, n} \in\{0,1\}, \quad \forall m \in \mathcal{A}, \quad \forall n \in \mathcal{T}_{m}$$

其中， $t_{m, n}$ 为App m的任务 n 的延迟需求， ε 为时隙的长度。 $t_{m,n}$ 可以由

$$t_{m, n}=\min \left(t_{l c}, \varepsilon\right)$$

其中 $t_{lc}$ 是卸载此任务的用户与无人机失去连接的时间。 C1 限制每个任务在当前时隙执行时的最大延迟。 C2 限制虚拟机的计算资源总和不能超过 C 。

可以看出，问题(14)是一个较难求解的混合整数规划。它涉及连续变量 C 和 0-1 整数变量 y 。即使我们假设 C 是已知的，残差子问题仍然是一个 0-1 整数约束的二次问题，对于非定阵 [28]，[29] ，残差子问题是NP难的。这个问题通常用特定的松弛方法来重新表述，然后用强大的凸优化技术来解决。然而，这种方法执行了大量的迭代，并揭示了很少的调度策略。因此，我们有动力设计一种高效的低复杂度算法来获得次优解。在本文提出的虚拟机分配和任务调度算法中，假设对于每个 VM m ，对 $N_m$ 任务的时延要求进行排序，即 $t_{m,n}≤t_{m,n+1}$。一开始，我们试图分配 $c_m$ ，就好像所有的任务都已经调度好了，即 $y_{m,n} = 1，\forall m \in A, \forall n \in T_m$ 。分配结果将是

$$c_{m}=\min \left\{\frac{n Z_{m}}{t_{m, n}}\right\}, \quad \forall m \in \mathcal{A}, \forall n \in \mathcal{T}_{m}$$

给定分配结果，如果 $\sum^M_{m=1} c_m > C$ ，这意味着不是所有的任务都可以被调度。因此，我们选择不安排延迟要求最苛刻的任务，即让

$$y_{m,n} = 0$$

式中，

$$m, n=\underset{m, n}{\arg \max } \frac{n Z_{m}}{t_{m, n}}, \quad \forall m \in \mathcal{A}, \quad \forall n \in \mathcal{T}_{m}$$

然后，我们再次计算 VM 分配 $c_m$ 。重复此过程，直到满足条件 $\sum^M_{m=1} c_m \le C$ ，得到虚拟机分配 $c_m$ 和任务调度 Y 。注意，对于一般的 Y ，虚拟机分配是按

$$c_{m}=\min \left\{\frac{\sum_{n} y_{m, n} Z_{m}}{t_{m, n}}\right\}, \quad \forall m \in \mathcal{A}, \quad \forall n \in \mathcal{T}_{m}$$

而非计划任务选择由

$$m, n=\underset{m, n}{\arg \max } \frac{\sum_{n} y_{m, n} Z_{m}}{t_{m, n}}, \quad \forall m \in \mathcal{A}, \forall n \in \mathcal{T}_{m} .$$

边缘服务器虚拟机分配和任务调度的完整算法如算法 1 所示。从算法中可以看出，最坏的情况(云无法及时完成任何卸载的任务)需要 $N^\prime (N^\prime + 1)/2$ 个比较，其中 $N^\prime$ 为分配给无人机边缘服务器的总任务数。即使在最坏情况下，复杂度 $O(N^{\prime2})$ 也很低，因此所提出的算法可以在动态 SAGIN 环境中有效地工作。

5.计算卸载问题公式

我们设计一个在线计算卸载方法 SAG-IoT 系统,在每个时间段的物联网设备的计算任务计划在本地处理,将无人机边缘服务器,通过卫星或卸载到云服务器,为了降低系统总成本任务的延迟、物联网用户的能耗以及 edge 和云服务器的使用成本。这可以通过将计算卸载决策建模为 MDP 来实现。

MDP 由一个元组 (S, A, T, R) 定义，其中 S 是系统可能状态的集合， A 是动作的集合， $T = {p(s^\prime|s, a)}$ 是转移概率的集合，R: S× A→R是当系统处于状态 s∈S ，且动作 a∈A 时的实值奖励(或代价)函数。策略 π 是 S 到 A 的映射。 SAG-IoT 计算卸载问题的 MDP 定义如下:

1)状态：从时刻 t 开始，网络状态定义为 $M(t)⊗T^r(t)⊗PL(t)⊗PL(t−1)⊗PL(t−2)⊗···⊗PL(t−t_q)$ ，即 $T^l_r(t) = \{t^l_1(t),t^l_2(t),\dots ,t^l_M (t)\}$ 表示每个用户完成本地处理任务的剩余时间，$PL(t) = {PL_1(t),PL_2(t), \dots ,PL_M(t)}$ 是所有用户到其关联无人机的路径损失值的向量。系统状态包括当前 $t_q$ 时隙和之前 $t_q$ 时隙的路径损耗信息，以学习和预测路径损耗信息。

2)行动:一开始的时间段 t ,系统需要操作的调度用户的任务,例如,确定矩阵 $X_l(t) X_e(t) $ 和 $X_c(t)$ 或同样确定 $x^l_{ij}, x^e_{ij},x^c_{ij},∀i,j$ 。因此,我们表示 $a(t) = {X_l(t),X_e(t),X_c(t)}$。显然，在时间槽 0 处，有 $4^{MN}$ 个可能的动作，当 M 和 N 都很大时，这是一个非常大的数。

3)迁移概率:由于UAV-user路径损失不受动作的影响，系统迁移概率可通过

$$p\left(s_{t+1} \mid s_{t}, a_{t}\right)=p(\mathbf{P L}(t+1) \mid \mathbf{P L}(t)) \cdot\left(\mathbf{T}_{r}^{l}(t+1) \mid \mathbf{T}_{r}^{l}(t), a_{t}\right) \cdot p\left(\mathbf{M}(t+1) \mid \mathbf{M}(t), a_{t}\right) .$$

具体来说，当规划无人机轨迹和飞行速度固定时，p(PL(t + 1)|PL(t)) 为 1 ，特定PL(t + 1)为1，否则为0。然而，由于无人机迁移率的不确定性，p(PL(t + 1)|PL(t))将难以建模。 $T^l_r(t + 1)$ 可由

$$T_{r, i}^{l}(t+1)=\max \left\{T_{r, i}^{l}(t)+\sum_{j=1}^{N} x_{i j}^{l}(t) \frac{Z_{j}}{\mathcal{C}^{l}}-\varepsilon, 0\right\}$$

对于 $p(M(t + 1)|M(t), a_t)$，很难精确建模。例如，将任务卸载到无人机边缘服务器，任务能否在时间段内完成，取决于无人机数据传输速率、无人机计算资源分配、其他用户决策、无人机移动性等，这些都是动态关联的。

4)奖励:为了最小化时延、能量和服务器使用成本的加权和，我们使用时间点 t 的成本函数 $C(s_t, a_t) = \sum_{i j} C_{i, j}\left(s_{t}, a_{t}\right)$ ，其中 $C_{i,j}(s_t, a_t)$ 是任务 $W_{ij}$ 的代价函数，计算方法如下:

1)如果 $m_{ij}(t) = 0$，则任务已经完成，因此 $C_{ij}(s_t, a_t) = 0$。

2)当 $m_{ij}(t) = 1$ 且 $x^l_{ij} + x^e_{ij} + x^c_{ij} = 0$ 时，该任务不在该时隙中调度，因此引入了 ε 的延迟。我们定义代价函数 $C_{ij}(s_t, a_t) = w_iε$ ，其中 $w_i$ 是用户 i 对延迟的权值。

3)如果$m_{i j}(t)=1$和 $x_{i j}^{l}+x_{i j}^{e}+x_{i j}^{c}=1, C_{i j}\left(s_{t}, a_{t}\right)= \
\varpi_{i}\left(x_{i j}^{l}\left(T_{i j}^{l}-\varepsilon t\right)+x_{i j}^{e}\left(T_{i j}^{e}-\varepsilon t\right)+x_{i j}^{c}\left(T_{i j}^{l}-\varepsilon t\right)\right)+x_{i j}^{l} L_{i j}^{l}+
x_{i j}^{e} L_{i j}^{e}+x_{i j}^{c} L_{i j}^{l} $

定义状态 s 的值函数 V 为策略 π 从 s 开始的期望长期折现成本，即:

$$V(s \mid \pi)=\mathbb{E}\left[\sum_{t=0}^{\infty} \gamma^{t} C\left(s_{t}, a_{t}\right) \mid s_{0}=s, \pi\right]$$

其中 γ∈[0,1] 是一个折扣因子，期望占据了从 s 开始的所有可能的状态轨迹。在线计算卸载方法是选择一个最优策略 π∗ ，它使每个状态的值函数最小化，即:

$$\left.\pi^{*}(s)=\arg \min \sum p\left(s^{\prime} \mid s, a\right)\left[C(s, a)+\gamma V\left(s^{\prime} \mid \pi^{*}\right)\right)\right]$$

6.基于RL的卸载决策

在问题(24)中，由于无人机的机动性和无人机边缘服务器VM的动态分配，奖励函数和转移概率难以准确建模。此外，随着系统尺度M和N的增大，系统状态空间呈指数增长，使得系统变得难以处理。因此，本文提出的在线计算卸载问题可以通过Q-learning[30]和策略梯度方法[31]等基于 RL 的无模型方法来解决。虽然Q-learning方法在解决RL问题的大状态空间方面表现出很大的潜力，但它通常不能有效地处理大的甚至是连续的行动空间问题，如问题(24)。因此，在本文中，我们提出了一种基于策略梯度法的 SAG-IoT 系统在线计算卸载方法。

提出了在线计算卸载方法,参数化的政策是一个向量 $θ∈R^d$ ,例如, $π(a|s,θ)= P (a_t = a|s_t= s,θ_t=θ)$ ,概率是采取行动当系统状态在时间 t ,政策下参数 θ 。对状态的每个特征定义为 θ ，即 M(t) ， $T^r(t)$ 和 PL(t) 中的每个元素，向量 θ 的长度为 $M(n + t_q + 2)$ 。为了学习政策参数，我们首先定义 θ 的性能测度，用 J(θ) 表示。由于在线计算卸载问题是偶发的(当所有MN任务完成时，一个事件结束)，我们将性能度量定义为计算所有任务的事件的总折扣成本。用 τ 表示 π(·|·，θ)之后的一段时间内状态-动作序列 $s_0,a_0,s_1,a_1,s_{t_{max}},a_{t_{max}}$ 的轨迹，其中 $t_max$ 为预设值，表示处理所有任务可能的最大时隙数。则有 J(θ) 为起始状态 $s_0$ 的值函数:

$$J(\boldsymbol{\theta}) \doteq V_{\pi_{\boldsymbol{\theta}}}\left(s_{0}\right)=\mathbb{E}_{\pi_{\boldsymbol{\theta}}}\left[\sum_{k=0}^{t_{\max }} \gamma^{k} C\left(s_{k}, a_{k}\right) \mid \pi(\cdot \mid \cdot, \boldsymbol{\theta})\right]$$

为了直观地学习使 J(θ) 最小的策略参数 θ ，我们可以用梯度下降法逐步更新 θ

$$\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_{t}-\varphi \nabla J\left(\boldsymbol{\theta}_{t}\right)$$

其中 $\varphi$ 表示学习速率。根据政策梯度定理，我们有

$$\begin{aligned} \nabla J\left(\boldsymbol{\theta}_{t}\right) &=\mathbb{E}_{\pi}\left[\sum_{a} q_{\pi}\left(s_{t}, a\right) \nabla_{\boldsymbol{\theta}} \pi\left(a \mid s_{t}, \boldsymbol{\theta}\right)\right] \\ &=\mathbb{E}_{\pi}\left[\sum_{a} \pi\left(a \mid s_{t}, \boldsymbol{\theta}\right) q_{\pi}\left(s_{t}, a\right) \frac{\nabla_{\boldsymbol{\theta}} \pi\left(a \mid s_{t}, \boldsymbol{\theta}\right)}{\pi\left(a \mid s_{t}, \boldsymbol{\theta}\right)}\right] \\ &=\mathbb{E}_{\pi}\left[q_{\pi}\left(s_{t}, a_{t}\right) \frac{\nabla_{\boldsymbol{\theta}} \pi\left(a_{t} \mid s_{t}, \boldsymbol{\theta}\right)}{\pi\left(a_{t} \mid s_{t}, \boldsymbol{\theta}\right)}\right] \\ &=\mathbb{E}_{\pi}\left[G_{t} \frac{\nabla_{\boldsymbol{\theta}} \pi\left(a_{t} \mid s_{t}, \boldsymbol{\theta}\right)}{\pi\left(a_{t} \mid s_{t}, \boldsymbol{\theta}\right)}\right] \end{aligned}$$

注意， $q_{\pi}\left(s_{t}, a\right)$ 是策略π的状态-动作值函数， $G_t = C_t+ \gamma C_{t+1}+\gamma ^2 C_{t+2} \dots$ 是成本的折现回报。利用上述方法，我们可以通过

$$\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_{t}-\varphi G_{t} \frac{\nabla_{\boldsymbol{\theta}} \pi\left(a_{t} \mid s_{t}, \boldsymbol{\theta}\right)}{\pi\left(a_{t} \mid s_{t}, \boldsymbol{\theta}\right)}$$

然而，这种更新方法(称为强化学习方法)虽然可以渐近收敛到局部最小值，但通常会导致方差较大，学习速度较慢。在在线 SAG-IoT 计算卸载中，状态空间和动作空间都很大，因此可能不适合采用强化学习方法。为了进一步提高学习性能，我们因此采用了行为者批评方法，其中策略函数和值函数的近似都是在[34]中学习的。在 Actor-Critic 方法中，策略在每个时隙中更新，而不是在计算卸载的每个阶段更新。因此，学习最优策略所需的样本数量可以大大减少，从而加快了学习过程。为了实现这一点，我们需要学习价值函数，并将其作为一个批评家来指导策略在每个时隙的更新。具体来说，用 $\hat V (s_t, ω)$ 表示状态 $s_t$ 的值函数的估计，式中 $ω∈R^m$ 是拟合值函数的参数向量。然后，在每个时隙 t 中， θ 的更新可由

$$\boldsymbol{\theta}_{t+1}=\boldsymbol{\theta}_{t}-\varphi\left(C_{t}+\gamma \hat{V}\left(s_{t+1}, \boldsymbol{\omega}\right)-\hat{V}\left(s_{t}, \boldsymbol{\omega}\right)\right) \frac{\nabla_{\boldsymbol{\theta}} \pi\left(a_{t} \mid s_{t}, \boldsymbol{\theta}\right)}{\pi\left(a_{t} \mid s_{t}, \boldsymbol{\theta}\right)}$$

注意，在每个时隙中，估值函数 $\hat V $ 的参数向量 ω 也按

$$\boldsymbol{\omega}_{t+1}=\boldsymbol{\omega}_{t}-\varphi^{\prime} \nabla_{\boldsymbol{\omega}} L(\boldsymbol{\omega})$$

式中 ϕ 为学习率，损耗函数 L(ω) 定义为

$$L(\boldsymbol{\omega})=\left|\hat{V}\left(s_{t}, \boldsymbol{\omega}\right)-\left(C_{t}+\gamma \hat{V}\left(s_{t+1}, \boldsymbol{\omega}\right)\right)\right|^{2}$$

最后，基于深度神经网络逼近复杂函数的能力，我们采用深度学习体系结构，根据θ和估计的状态值函数学习策略。完整建议的 SAT-IoT 在线计算卸载方法在算法2中显示，其中φ和 $φ^\prime$ 分别是演员和评论家的学习率。

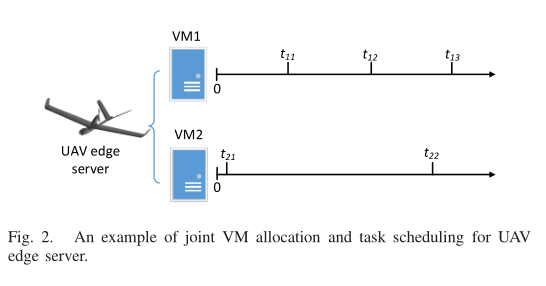
本文提出的基于 RL 的卸载方法的实现如图 3 所示，该方法由 SAGIN 环境、计算卸载奖励评估器、参与者网络、评论网络和时间差组件组成。系统状态可以从当前的 SAGIN 环境中观察到，然后发送到参与者网络和批评网络的输入。行动者网络根据 $a = π_θ(s)$ 生成动作 a ，并更新策略 θ 。可以很容易地看到，在时间点 t , f 或 n 个任意任务 $W_{ij}$ 时，决策 $x_{ij}(t)$ 有四种可能性，即不调度、本地处理、卸载到边缘和卸载到云。因此，我们将这四种可能的决策分别映射到 $x_{ij}$ 整数 0,1,2,3，并设计行动者网络的输出层，即 σ 和 μ ，它们可以组成 M × N 个正态分布随机变量来表示每个任务的行为。批评家网络估算值函数 $\hat V (s_t, ω)$ 并更新参数 ω 。一双政府行动的报酬奖励评估者的评估,并用于计算 temporal-difference (TD) $ \eta= C_{t}+\gamma \hat{V}\left(s_{t+1}, \boldsymbol{\omega}\right)-\hat{V}\left(s_{t}, \boldsymbol{\omega}\right) $ ,用于更新的政策参数θ和评论家网络参数ω。

7.性能验证

A.模拟配置

在本节中，我们评估了针对无人机边缘服务器提出的联合虚拟机资源分配和任务调度方案，以及基于 rl 的 SAT-IoT 系统在线计算卸载方法。在模拟中，我们考虑一个偏远的1 km × 1 km平方的区域，该区域固定部署 M = 30 个物联网用户。物联网用户运行 N = 5 个不同的应用程序，因此每个用户有 5 个任务要处理。地面用户选择基于 ARM Cortex-M 的物联网设备。参照[35]和[36]，我们将物联网设备计算能力 Cl 设置为 200 MC/s (MC = 1 06 cycles) ，本地任务处理能耗为 141 mW。如[37]中定义的，设置拥有无人机和卫星的物联网用户的传输和接收功率，即 $E^e$ , $E^{e−}$ 和 $E^c$ 为 200mW 。 5 架无人机将作为物联网计算的飞行边缘服务器。采用实际的无人机-地面传播信道(1)，规划无人机的运动轨迹，使Wu等人的工作[38]之后的最小吞吐量最大化。边缘服务器的计算资源 $C^e$ 将 3 GC/s (GC = $10^9$ cycles),而云服务器的计算资源分配给每一个任务,例如 $C^c$ 被设置为 10 GC/s。卫星和远程云,我们考虑在一个集计算卸载,有一个 LEO 卫星提供的完整覆盖区域,和卫星地面通信速率显示设置为 10 Mbps 的平均观测传输速度高吞吐量 ViaSat-1 卫星通信系统。卫星云数据传输速率也受到卫星地面传输速率的限制，因此我们设置 $r_{SC} = r_{SG} = 10 Mbps$ 。不同的计算任务可能有不同的计算与数据比率;但是，为了模拟的简单性，我们选择 x264 VBR编码计算与数据的比率，即 1300 cycles/byte ，即Z = 1300Hin[40]。 $H^{in}_j$ 和 $H^{out}_j$ 分别在 5mb 和 15mb 之间， 1mb 和 5mb 之间随机选择。我们将边缘服务器/云服务器的使用成本，即 $B^e_{ij}$ 和 $B^{c}_{ij}$ ，设为执行任务 $W_{ij}$, i的CPU周期。另外，对于每个用户i， α = $10^{-10}$ J/cycle， β = 4 × $10^{-10}$ J/cycle, $w_i$ = 1 J/s。详细的仿真参数如表 2 所示。

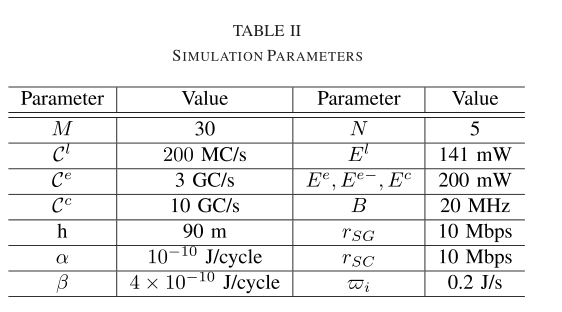
B.虚拟机计算资源分配与调度

首先对所提出的虚拟机计算资源分配和任务调度算法进行了评估。我们将启发式算法与“蛮力”方法和“随机”方法进行了比较。在“蛮力”中，用穷举搜索来寻找最优的计划外任务，虽然性能上界，但计算复杂度较高。在“随机”中，计划外的任务是随机选择的。

本文算法的延迟性能如图4所示。图4(a)为相对于无人机边缘服务器计算资源 $C^e$ 的平均延迟。从图中我们可以看出，随着 $C^e$ 的增加，这三种方法的平均时延都在减小，因为计算服务器能力越强，平均处理时间就会越短，从而可以调度更多的任务来满足它们的时延要求。在图4(b)中，显示了当 $C^e$ 设置为10 GC时，相对于卸载到考虑的边缘服务器的总任务数的平均延迟。从图中可以看出，任务数量越多，平均延迟越长，因为更多的任务会争夺有限的计算资源，能够按时完成的任务就越少。在两幅图中，提出的启发式算法可以实现与“暴力破解”方法非常接近的性能，这证明了提出的算法的效率。

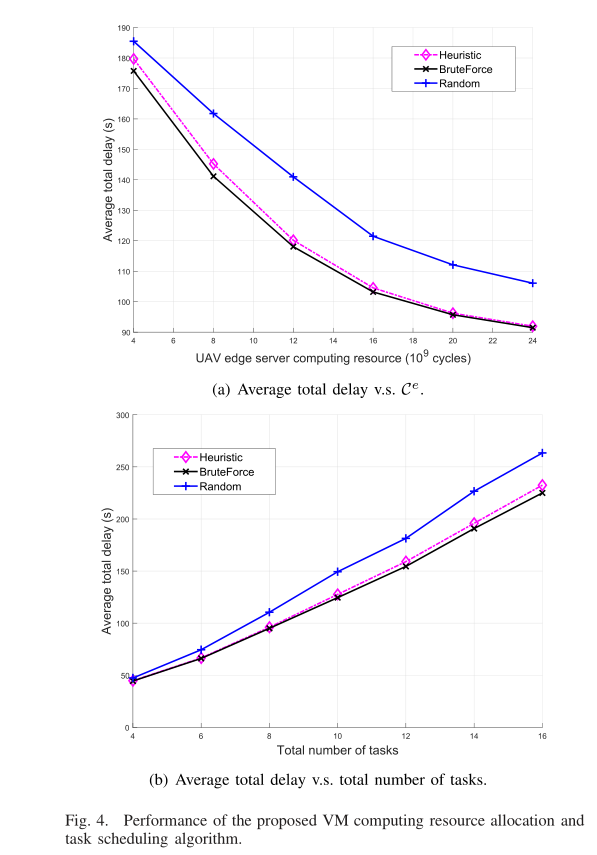
图 5 显示了所提启发式算法和“蛮力”方法的运行时间比较。从图中我们可以看出，随着总任务数的增加，“蛮力”方法的运行时间呈指数增长。这是因为“蛮力”方法使用了穷举搜索，大量的任务导致搜索空间呈指数增长。相反，当任务数量增加时，启发式算法的运行时间保持非常小。放大后的启发式算法的运行时间显示，当卸载任务数量增加时，运行时间明显呈二次型增长，这验证了我们在第四节中的分析。综上所述，所提出的虚拟机计算资源分配和任务调度算法能够同时实现接近最优的性能和非常低的计算复杂度，适合于动态网络条件下无人机边缘服务器资源的分配。

C.基于深度 RL 的物联网计算卸载

本部分对基于 RL 的 SAG-IoT 计算卸载方法的性能进行了评估和比较。为了证明我们提出的方法的有效性，我们明确地将其与另外两种计算卸载方法，即“Random”和“Greedy on edge”进行了比较，如下所示。

1)“Random”:每个任务随机选择一个时间段 $t∈{1,2,\dots,t_{max}}$ ，和卸载决策(本地，边缘，云)。

2)“Greedy on edge”:由于边缘计算通常可以提供较低的计算延迟和相对较低的价格，每个用户在无人机的覆盖范围内，将所有的任务都转移到无人机的边缘服务器上。否则，用户决定等待、本地处理或以一定的概率卸载到云。在模拟中，我们分别将概率设置为0.8、0.1和0.1。

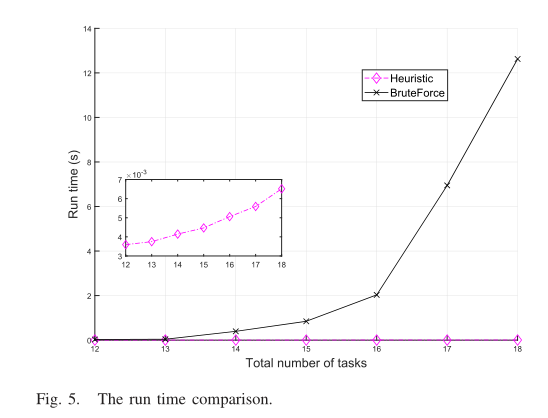
本文提出的基于 RL 的计算卸载算法的收敛性能如图6所示。总成本是每个任务的成本之和，即延迟成本、能耗成本和服务器使用成本的加权和。从算法在第10次循环左右已经收敛的事实可以看出，该算法收敛速度非常快。收敛速度高的原因是采用了actor-critic算法，在该算法中，评论家网络在每个时间段内判断并引导演员网络学习策略，而非actor-critic算法策略梯度方法在每个时段学习策略。算法的快速收敛可以带来很多好处，如部署更多用户和应用程序时可以快速重新配置，在动态环境中具有更大的灵活性等。

图7显示了本文提出的计算卸载方法对无人机服务器使用成本权重α的性能。可以看出，本文提出的基于RL的方法能够通过与环境的交互来学习最优的卸载策略，因此与其他方法相比，该方法的总成本最低。在这三种方法中，“贪心”方法的总成本最高。这是因为“贪心”方法迫使无人机信道和边缘服务器的计算资源占用了很多任务内容，增加了任务的完成时间。此外，由于无人机的机动性，在任务处理(包括上传、处理、传输结果)的时间内，无人机可能会飞走，用户失去连接。

在图8中，成本的主要组成部分，即能耗(E + B·α(或β))和时延权重(wT) 表示。可以看出，由于学习了最优卸载策略，所提出的计算卸载方法能够达到最低的能耗和最低的延迟。“随机”方法能够实现与基于RL的方案相似的总延迟的原因是，在基于RL的方案中，将任务发送给卫星需要消耗更多的能量，而在随机方案中，在“随机”方法下，由于更多的任务是在局部处理的，因此局部进程延迟更长，因此在局部处理任务时会消耗更多的能量(如图10所示)。然而，“贪婪”方法的能量消耗和延迟非常高，这是由于无人机边缘服务器上的任务执行失败，导致同一任务的多次上传，从而消耗了物联网设备的大量能量，导致延迟时间延长。

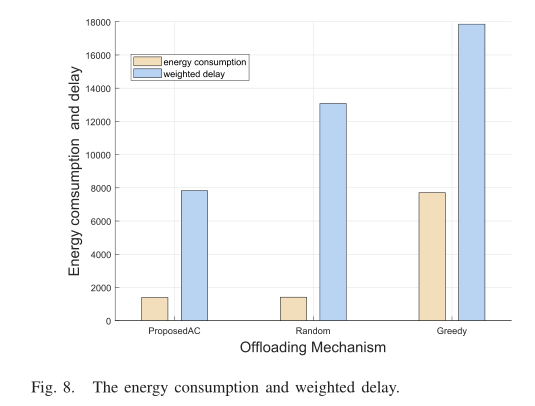
图9显示了相对于云服务器使用成本权重β的总成本。通过比较这三种方法，可以发现基于RL的计算卸载方法可以达到最小的平均总成本。总成本随着β的增加而增加，因为β的增加会导致总成本的组成部分$βB^c$的增加。也可以看出，本文方法的总成本比其他两种方法增加得更快，这是因为在当前的仿真设置中，如果选择得当，卫星云卸载可以比局部处理和无人机获得相对更好的性能。因此，该方法能够学习环境，选择概率较高的云卸载方法。这一事实可以在图10中看到，图10显示了每种卸载方法的每种卸载方式的选择数量。对于所提出的方法，它更频繁地选择卫星云而不是其他两种卸载方式。与卫星云相比，局部处理由于具有较强的本地计算能力而导致较长的延迟，而无人机边缘虽然具有较高的传输速率和较低的服务器使用成本，但可能会面临竞争问题和较高的无人机机动性。“随机”和“贪婪”方法选择了几乎相同数量的本地处理和卫星云。“贪婪”方法选择无人机边缘的次数更多，因为如果无人机当前不可用，它可能会等待未来无人机连接，且概率较高。

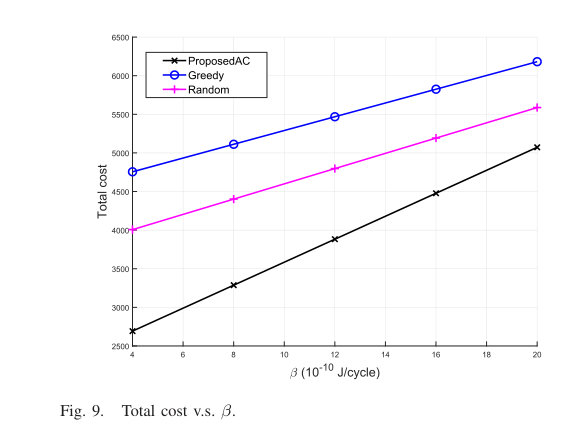
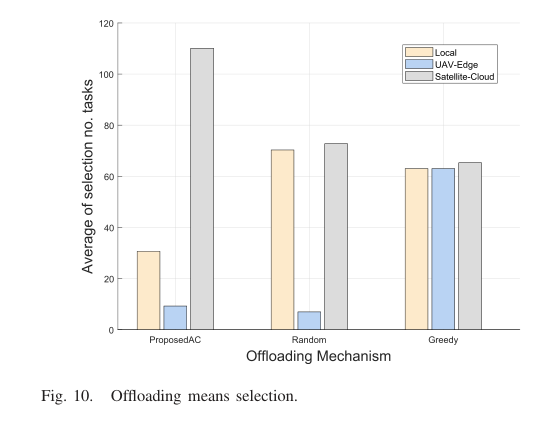
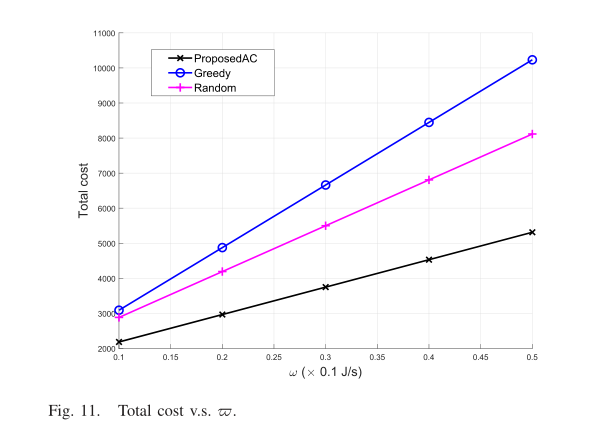
图11显示了相对于延迟权重的总成本w。随着w的增加，三种卸载方式的总成本都增加，原因是wT(总成本的延迟部分)的增加。然而，由于该方法能够从环境中学习最优策略以减少总任务延迟，因此在三种方法中总成本最低，增长率也较低。

8.结论

在本文中，我们研究了SAGIN中的物联网计算卸载问题。提出了一种虚拟机联合分配和任务调度机制，有效地将计算资源分配给无人机边缘服务器中的不同虚拟机。为了减轻计算密集型任务的负担，我们提出了一种基于RL的计算卸载方法来处理多维SAGIN资源并学习动态网络条件。深度神经网络、策略梯度和行为者批评方法已被用于提高学习性能。仿真结果验证了该方法的收敛性和有效性。我们的工作可以为SAGIN中重要但尚未开发的边缘/云计算领域提供有价值的见解。在未来，我们将专注于共同优化SAGIN中的通信、缓存和计算资源。