无人机辅助移动边缘计算中的节能资源管理

摘要：无人机的部署增强了网络容量，并为移动用户提供服务，无论其是否有基础设施覆盖。与此同时，我们观察到物联网设备和应用呈指数级增长。然而，由于物联网设备的计算能力和电池寿命有限，因此在设备上本地处理数据具有挑战性。为此，本文提出了一种无人机辅助移动边缘计算系统。通过优化任务卸载决策、资源分配机制和无人机轨迹，同时考虑通信和计算延迟要求，研究了物联网设备和无人机在任务执行过程中的能耗联合最小化问题。揭示了该问题的非凸结构，并证明其求解具有挑战性。为了应对这一挑战，提出了一种块连续上界最小化（BSUM）算法。最后，通过仿真验证了算法的有效性。

1.简介

随着可穿戴设备、计量设备、流量和其他监测设备等物联网设备的迅速普及，对智能农场、人脸识别、在线游戏、虚拟现实( VR )和增强现实( AR )等计算密集型应用的支持需求也在不断增加。此外，物联网设备是低功耗设备，计算能力有限。因此，这类物联网设备在本地执行计算任务具有挑战性。解决这一挑战的一种有希望的方法是部署边缘服务器，使计算资源离设备更近，并通过将设备的计算任务转移到本地移动边缘计算( MEC )服务器来降低设备的能源消耗。然而，在一些应用中，如农村智能农业、灾害救援行动、军事行动等，物联网设备距离移动边缘计算服务仍有很大距离，且处于蜂窝系统覆盖范围之外，无法使用 MEC 服务。最近，为了扩大蜂窝网络的覆盖范围，并向尚未部署蜂窝基础设施的移动设备提供网络服务，无人机( UAVs )被广泛应用。在文献[4]中，作者研究了无人机辅助移动边缘计算系统的计算效率最大化问题，文献[5]中考虑了将任务卸载到邻近无人机的策略，以实现类似雾的计算平台。然后，文献[6]提出了一种基于无人机的移动边缘计算系统的联合卸载和轨迹优化设计方法。特别地，作者关注于最小化移动设备所经历的延迟。而在文献[6]中，作者认为每个移动设备的传输功率是恒定的，忽略了任务执行时的计算资源分配。同时，在文献[7]中，研究了潜伏期对细胞关联的影响。在文献[8]中，通过联合优化任务调度和资源分配，考虑无人机整体能量最小化问题。然而，在文献[8]中并未考虑物联网设备的能耗。

本文的主要贡献在于，通过优化任务卸载决策、资源分配机制和无人机轨迹，在满足移动设备延迟需求的同时，开发了一种新的最小化总能耗的框架。为了解决公式化的非凸问题，我们采用 BSUM 方法。仿真结果表明，该算法的总能耗比基于块坐标下降( Block Coordinate Descent, BCD )的方案、等价资源分配方案和远程任务执行方案分别降低了 10.54%、18.49%和40.67% 。

2.系统模型

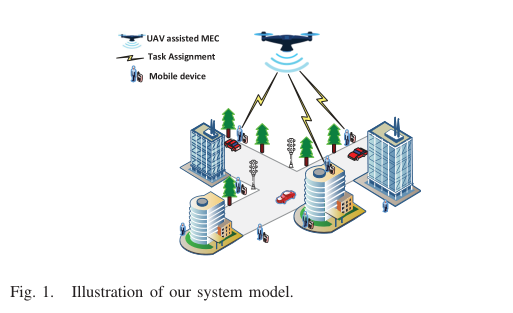
在图 1 中，无人机辅助的 MEC 系统是用一个单一的无人机作为空中基站。空中基站集成了一个边缘服务器，同时还提供一组物联网设备 U 。为了向地面移动设备提供计算服务，无人机(空中基站)盘旋在地面移动设备的上方。无人机能够在飞行期间的任何给定时间同时与地面移动设备通信并提供计算服务。

随着更长的飞行周期 T , 无人机有更多的时间飞近每个地面设备，实现更好的空对地链接。假设各地面设备的横坐标提前已知，固定 $\boldsymbol{o}_{u}=\left[x_{u}, y_{u}\right]^{T}, \forall u \in \mathcal{U}$ 。无人机固定高度 H 飞行，水平坐标 $\boldsymbol{c}(t)=[x(t), y(t), H]^{T}, 0 \leq t \leq T$ 。然后，我们将无人机飞行周期 T 离散为 N 个间隔相等的时隙集，每个时隙的长度设为 $L = \frac{T}{N}$ 。此外，为了定期向地面移动设备提供计算服务，并为无人机充电，我们假设无人机需要在飞行周期结束时返回到初始位置，即 c(1) = c(N) 。无人机的最大速度表示为 V 。然后，我们有以下约束，以确保无人机在每个时隙的速度低于其最大速度:

$$\frac{\|\boldsymbol{c}(n+1)-\boldsymbol{c}(n)\|}{L} \leq V, \quad \forall n \in \mathcal{N}$$

此外，我们可以看到 LV 是无人机在每个时间槽中所能走的最大距离。然后，无人机从一个地方到另一个地方的能量消耗与无人机的速度有关。在此情况下，文献 [9] 中所描述的无人机在每个时隙移动的能量消耗如下:

$$E^{\mathrm{fly}}(n)=k\left(\frac{\| \boldsymbol{c}(n+1)-\boldsymbol{c}(n)) \|}{L}\right), \quad \forall n \in \mathcal{N}$$

其中 k = 0.5M , M 为无人机的有效载荷。此外，假设在时间槽 n 内无人机到接地设备 u 的距离为常数，由:

$$d_{u}(n)=\sqrt{H^{2}+\left\|\boldsymbol{c}(n)-\boldsymbol{o}_{u}\right\|^{2}}, \quad \forall u \in \mathcal{U}, \forall n \in \mathcal{N}$$

在本文中，我们考虑了移动设备与无人机之间的准静态块衰落信道模型。这意味着通道在块内保持不变，并且可能在不同块上发生变化。此外，根据文献[10]，地面移动设备与无人机之间会有较强的视距(Line of Sight, LOS)链路，当无人机处于足够高的高度时，由于散射，链路会出现小尺度的衰落。在块衰落信道模型下，我们可以将器件 u 在 n 时刻的信道系数建模为 $h_{u}(n)=\sqrt{\zeta_{u}(n)} \rho_{u}(n)$ ， 式中 $\zeta_{u}$ 为平均信道功率增益， $\rho_{u}(n)$ 为小尺度信道系数。那么，平均信道功率增益 $\zeta_{u}$ 可以表示为:

$$\zeta_{u}(n)=\zeta_{0} d_{u}^{-\theta}(n)=\frac{\zeta_{0}}{\left(H^{2}+\left\|\boldsymbol{c}(n)-\boldsymbol{o}_{u}\right\|^{2}\right)^{\theta / 2}}$$

式中， $\zeta_{0}$ 是参考距离 $d_0=1m$ 处的平均信道功率增益， $\theta$ 是路径损耗指数。 此外， c(n) 和 ${o}_{u}$ 分别表示无人机和设备 u 在时隙 n 处的位置。然后，由于存在强视距链路，我们可以使用Rician分布（即Rician衰落）对小范围衰落进行建模，如下所示：

$$\rho_{u}(n)=\sqrt{\frac{K_{u}(n)}{K_{u}(n)+1}} \rho+\sqrt{\frac{1}{K_{u}(n)+1}} \hat{\rho}$$

式中， $\rho$ 表示 $|\rho|=1$ 的确定性服务水平分量， $\hat{\rho}$ 表示被假定为零平均单位方差圆对称复高斯（CSCG）随机变量的随机散射分量， $K_{u}(n)$ 是Rician因子。

A.本地计算模型

每个移动设备都有一个任务要在每个时隙 n 执行，该时隙 n 由元组 $\left\{\beta_{u}, a_{u}(n), T_{u}(n)\right\}$ 表示，其中 $\beta_{u}$ 是计算 1 位输入数据所需的 CPU 周期， $a_{u}(n)$ 是总输入数据大小， $T_{u}(n)$ 是完成任务所需的时间量。由于移动设备受到功率和计算能力的限制，因此不可能在本地执行所有任务。一个很有前景的解决方案是将移动设备任务的一小部分分配给无人机，该无人机与板上具有更强大的计算能力的边缘服务器相连。使用 $l_u(n)$和 $(a_u(n)-l_u(n))$ 分别表示在无人机上远程执行的任务和在移动设备 u 上本地执行的部分任务。对于每个时隙 n ，设备 u 的本地计算延迟/延迟由文献[6]计算，如下所示：

$$t_{u}^{l}(n)=\frac{\beta_{u}\left(a_{u}(n)-l_{u}(n)\right)}{f_{u}^{l}}, \quad \forall u \in \mathcal{U}, \forall n \in \mathcal{N}$$

其中 $f^l_u$ 是用户 u 的最大计算容量（即循环/s）。然后，设备 u 在时隙 n 的本地能耗由文献[6]给出，如下所示：

$$E_{u}^{l}(n)=w\left(f_{u}^{l}\right)^{2} \beta_{u}\left(a_{u}(n)-l_{u}(n)\right), \quad \forall u \in \mathcal{U}, \forall n \in \mathcal{N}$$

其中 w 是一个常数，取决于移动设备的芯片结构，我们将设置 $w=5×10^{−27}$ 如[6]所定义。

B.无人机辅助边缘计算模型

当每个移动设备的任务分配给无人机辅助的 MEC 服务器时，系统带宽的一小部分分配给每个移动设备。现在我们引入变量 B 和αu（n），分别表示总系统带宽和在时隙n分配给设备u的部分系统带宽。然后，设备u在时隙n的瞬时信道容量将为：

$$C_{u}(n)=\alpha_{u}(n) B \log _{2}\left(1+\frac{p_{u}(n)\left|h_{u}(n)\right|^{2}}{\sigma^{2}}\right), \quad \forall u, \forall n$$

其中， $p_{u}(n)$ 是用户 u 在时隙 n 处的发射功率， $\sigma^{2}$ 是加性高斯噪声功率。然后，设备 u 和无人机在时隙 n 处的中断概率如下：

$$\begin{aligned} P_{u}^{\text {out }}(n) &=\mathbb{P}\left(C_{u}(n)<R_{u}(n)\right) \\ &=F\left(\frac{\sigma^{2}\left(2^{R_{u}(n) /\left(\alpha_{u}(n) B\right)}-1\right)}{\zeta_{u}(n) p_{u}(n)}\right) \end{aligned}$$

其中， $F(\cdot)$ 是随机变量 $|p_{u}(n)|^2$ 的累积分布函数（CDF）， $P_{u}^{\text {out }}(n)$ 是关于 $R_{u}(n)$ 的非减量函数。此外，中断概率 $P_{u}^{\text {out }}(n)= \epsilon$ ，其中 $ \epsilon$ 是最大中断容许概率。最后，设备 u 在时隙 n 处的中断感知可实现数据速率可以表示为：

$$R_{u}(n)=\alpha_{u}(n) B \log _{2}\left(1+\frac{F^{-1}(\epsilon) p_{u}(n) \zeta_{0}}{\sigma^{2}\left(H^{2}+\left\|\boldsymbol{c}(n)-\boldsymbol{o}_{u}\right\|^{2}\right)^{\theta / 2}}\right)$$

其中， $F^{-1}(\cdot)$ 是互补累积分布函数（即 $F(\cdot)$ 的逆函数）。

然后，当在时隙 n 处将任务 $l_u(n)$ 的部分分配给无人机时，我们可以得到移动设备 u 的上行链路传输时间，其在文献[6]中描述如下：

$$t_{u}^{\mathrm{up}}(n)=\frac{l_{u}(n)}{R_{u}(n)}, \quad \forall u \in \mathcal{U}, \forall n \in \mathcal{N}$$

此外，当无人机在时隙 n 处被分配部分任务 $l_{u}(n)$ 时，上行链路传输（从移动设备到无人机）的能耗如下所述（文献[6]）：

$$E_{u}^{\mathrm{up}}(n)=\frac{p_{u}(n) l_{u}(n)}{R_{u}(n)}, \quad \forall u \in \mathcal{U}, \forall n \in \mathcal{N}$$

然后，在文献[6]中描述的时隙 n 处，在无人机处执行用户 u 的分配任务所需的计算时间/延迟如下：

$$t_{u}^{\operatorname{comp}}(n)=\frac{\beta_{u} l_{u}(n)}{f_{u}^{C}(n)}, \quad \forall u \in \mathcal{U}, \forall n \in \mathcal{N}$$

式中， $f_{u}^{C}(n)$ 是安装在无人机上的服务器在时隙 n 分配给设备 u 的计算能力（即循环/s）。然后，无人机在时隙 n 执行与设备 u 相关的部分任务所消耗的能量，如文献[6]所述：

$$E_{u}^{\text {exe }}(n)=q\left(f_{u}^{C}\right)^{2} \beta_{u} l_{u}(n), \quad \forall n \in \mathcal{N}$$

其中 q 是一个常数，取决于无人机边缘服务器的芯片架构，我们按文献[6]中的定义进行设置 $q=5×10^{−27}$ 。研究发现，在无人机 MEC 服务器上执行分配任务后，输出数据的大小明显小于分配任务的大小。另一方面，分配给下行链路传输的带宽远大于上行链路传输的带宽。因此，在将输出数据发送回设备 $u\in U$ 时，下行链路传输的延迟/延迟和能量消耗被认为是微不足道的。因此，在本研究中，无人机到地面设备的下行链路传输被省略。

3.节能任务分配与资源分配

根据第二节的模型，我们的目标是研究无人机辅助移动边缘计算系统中的联合任务分配和资源分配问题，以最小化地面移动设备和无人机的能耗。

据我们所知，我们的工作是通过联合优化无人机的轨迹、通信和计算资源分配以及任务分配，首先考虑移动设备及其服务无人机的能量最小化。我们可以正式提出以下问题：

$$\begin{array}{l} \min _{c, l, \boldsymbol{\alpha}, \boldsymbol{p}, \boldsymbol{f}}\left(\sum_{n=1}^{N} \sum_{u=1}^{U} E_{u}^{l}(n)+E_{u}^{\mathrm{up}}(n)\right)+\sum_{n=1}^{N} E^{\mathrm{fly}}(n) \\ \quad+\sum_{n=1}^{N} \sum_{u=1}^{U} E_{u}^{\mathrm{exe}}(n) \\ \text { s.t. } t_{u}^{\mathrm{up}}(n)+t_{u}^{\mathrm{comp}}(n) \leq T_{u}(n), \quad \forall u \in \mathcal{U}, \forall n \in \mathcal{N}, \\ t_{u}^{l}(n) \leq T_{u}(n), \quad \forall u \in \mathcal{U}, \forall n \in \mathcal{N}, \\ l_{u}(n) \leq a_{u}(n), \quad \forall u \in \mathcal{U}, \forall n \in \mathcal{N}, \\ \sum_{u=1}^{U} f_{u}^{C}(n) \leq f^{C}(n), \quad \forall n \in \mathcal{N}, \\ 0 \leq p_{u}(n) \leq p_{u}^{\max }(n), \quad \forall n \in \mathcal{N}, \forall u \in \mathcal{U}, \\ \sum_{u=1}^{U} \alpha_{u}(n) \leq 1, \quad 0 \leq \alpha_{u}(n) \leq 1, \forall u \in \mathcal{U}, \forall n \in \mathcal{N}, \\ \frac{\|\mathbf{c}(n+1)-\mathbf{c}(n)\|}{L} \leq V, \quad \forall n \in \mathcal{N}, \\ \boldsymbol{c}(1)=\boldsymbol{c}(N), \quad \end{array}$$

式中公式 (15a) 和公式 (15b) 表示每个移动设备任务在每个时隙的延迟约束，公式 (15c) 保证设备 u 分配给无人机的任务的比例始终小于设备任务的总输入数据大小。公式 (15d) 和公式 (15e) 分别表示无人机的计算能力约束和各地面移动设备的功率约束。公式 (15f) 捕获每个时隙 n 分配给设备的总带宽 B 的部分。最后公式 (15g) 为无人机的速度约束，公式 (15h) 确保无人机在飞行期间结束时返回到初始位置。

由于目标函数中大量决策变量与非线性约束及其非凸结构之间的耦合，利用凸优化技术求解公式(15)中的优化问题具有挑战性。因此，我们采用 BSUM 算法求解公式(15)[11]。 BSUM 算法连续地最小化目标函数的紧上界序列，并依次更新变量 $c,l,\alpha,p,f$ ，并保证 BSUM 收敛于公式(15)中的目标函数的驻点集合。为了应用 BSUM 方法，我们可以将式 (15) 中的优化问题更简洁地重写为:

$$\min _{\boldsymbol{c} \in \mathcal{C}, l \in \mathcal{L}, \alpha \in \alpha, \atop \boldsymbol{p} \in \mathcal{P}, \boldsymbol{f} \in \mathcal{F}} \mathcal{O}(\boldsymbol{c}, \boldsymbol{l}, \boldsymbol{\alpha}, \boldsymbol{p}, \boldsymbol{f})$$

式中， $\mathcal{O}(\boldsymbol{c}, \boldsymbol{l}, \boldsymbol{\alpha}, \boldsymbol{p}, \boldsymbol{f})=\left(\sum_{n=1}^{N} \sum_{u=1}^{U} E_{u}^{l}(n)+E_{u}^{\mathrm{up}}(n)\right)+ \sum_{n=1}^{N} E^{\mathrm{fly}}(n)+\sum_{n=1}^{N} \sum_{u=1}^{U} E_{u}^{\mathrm{exe}}(n)$ 。而且， $\mathcal{C} \triangleq\left{\boldsymbol{c}: t_{u}^{{\mathrm{up}}(n)+t_{u}}{\mathrm{comp}}(n) \leq T_{u}(n), \frac{|\mathbf{c}(n+1)-\mathbf{c}(n)|}{L} \leq V,\right. , \forall u \in \mathcal{U}, \forall n \in \mathcal{N}} $ ， $\begin{aligned} \mathcal{L} \triangleq &\left\{\boldsymbol{l}: t_{u}^{\text {up }}(n)+t_{u}^{\text {comp }}(n) \leq T_{u}(n), t_{u}^{l}(n) \leq T_{u}(n), l_{u}(n) \leq\right. \left.a_{u}(n), \forall u \in \mathcal{U}, \forall n \in \mathcal{N}\right\} \end{aligned}$ ， $\alpha \triangleq\left\{\boldsymbol{\alpha}: t_{u}^{\mathrm{up}}(n)+t_{u}^{\mathrm{comp}}(n) \leq T_{u}(n), \sum_{u=1}^{U} \alpha_{u}(n) \leq 1,0 \leq \alpha_{u}(n)\right. \leq 1, \forall u \in \mathcal{U}, \forall n \in \mathcal{N}\}$ ， \mathcal{P} \triangleq &\left\{\boldsymbol{p}: t_{u}^{\mathrm{up}}(n)+t_{u}^{\mathrm{comp}}(n) \leq T_{u}(n), 0 \leq p_{u}(n) \leq p_{u}^{\max }(n), \forall n,\right.\forall u \in \mathcal{U}\}\\ ， $\mathcal{F} \triangleq \left\{\boldsymbol{f}: t_{u}^{\mathrm{up}}(n)+t_{u}^{\mathrm{comp}}(n) \leq T_{u}(n), \sum_{u=1}^{U} f_{u}^{C}(n) \leq f^{C}(n), \forall u,\right. \forall n \in \mathcal{N}\}$ ,分别是 $c,l,\alpha,p,f$ 的可行集。在每次迭代 k 时， $\forall i\in I^k$ ，其中 $I$ 为索引集，我们定义式(16)中目标函数的近端上界函数 $O_i$ ，加上二次惩罚项使近端上界函数保持凸性，如下所示:

$$\mathcal{O}_{i}\left(\boldsymbol{c}_{i} ; \boldsymbol{c}^{k}, \boldsymbol{l}^{k}, \boldsymbol{\alpha}^{k}, \boldsymbol{p}^{k}, \boldsymbol{f}^{k}\right)=\mathcal{O}\left(\boldsymbol{c}_{i} ; \tilde{\boldsymbol{c}}, \tilde{\boldsymbol{l}}, \tilde{\boldsymbol{\alpha}}, \tilde{\boldsymbol{p}}, \tilde{\boldsymbol{f}}\right)+\frac{\mu_{i}}{2}\left\|\left(\boldsymbol{c}_{i}-\tilde{\boldsymbol{c}}\right)\right\|^{2}$$

其中 $\mu_{i}$ 是一个正惩罚参数，对于变量 $l_i,\alpha_i,p_i,f_i$ 的其他向量， $\mu_{i}$ 都可以展开。此外,近端上限函数(17)在每次迭代 k 中对 $c_i,l_i,\alpha_i,p_i,f_i$ 有一个独特的最小值向量 $\tilde{\boldsymbol{c}}, \tilde{\boldsymbol{l}}, \tilde{\boldsymbol{\alpha}}, \tilde{\boldsymbol{p}}, \tilde{\boldsymbol{f}}$ ,考虑到上一次迭代的解决方案(k−1)。然后,在每个迭代 (k + 1) 的解决方案可以更新通过求解子问题如下:

$$\begin{array}{l} \begin{array}{l} \boldsymbol{c}_{i}^{(k+1)} \in \min _{c_{i} \in \mathcal{C}} \mathcal{O}_{i}\left(\boldsymbol{c}_{i} ; \boldsymbol{c}^{(k)}, \boldsymbol{l}^{(k)}, \boldsymbol{\alpha}^{(k)}, \boldsymbol{p}^{(k)}, \boldsymbol{f}^{(k)}\right) \\ \boldsymbol{l}_{i}^{(k+1)} \in \min _{\boldsymbol{l}_{i} \in \mathcal{L}} \mathcal{O}_{i}\left(\boldsymbol{l}_{i} ; \boldsymbol{l}^{(k)}, \boldsymbol{c}^{(k+1)}, \boldsymbol{\alpha}^{(k)}, \boldsymbol{p}^{(k)}, \boldsymbol{f}^{(k)}\right) \\ \boldsymbol{\alpha}_{i}^{(k+1)} \in \min _{\boldsymbol{\alpha}_{i} \in \alpha} \mathcal{O}_{i}\left(\boldsymbol{\alpha}_{i} ; \boldsymbol{\alpha}^{k}, \boldsymbol{c}^{(k+1)}, \boldsymbol{l}^{(k+1)}, \boldsymbol{p}^{(k)}, \boldsymbol{f}^{(k)}\right) \\ \boldsymbol{p}_{i}^{(k+1)} \in \min _{\boldsymbol{p}_{i} \in \mathcal{P}} \mathcal{O}_{i}\left(\boldsymbol{p}_{i} ; \boldsymbol{p}^{(k)}, \boldsymbol{c}^{(k+1)}, \boldsymbol{l}^{(k+1)}, \boldsymbol{\alpha}^{(k+1)}, \boldsymbol{f}^{(k)}\right) \end{array}\\ \boldsymbol{f}_{i}^{(k+1)} \in \min _{\boldsymbol{f}_{i} \in \mathcal{F}} \mathcal{O}_{i}\left(\boldsymbol{f}_{i} ; \boldsymbol{f}^{(k)}, \boldsymbol{c}^{(k+1)}, \boldsymbol{l}^{(k+1)}, \boldsymbol{\alpha}^{(k+1)}, \boldsymbol{p}^{(k+1)}\right) \end{array}$$

此外，公式(18)-(20)中的子问题可以用 BSUM 算法求解。

4.模拟结果

在我们的模拟中，我们考虑与 MEC 服务器相连的无人机在固定高度 H = 20 m 飞行，最大速度 V = 7 m/s ，覆盖面积为 $(70 × 70) m^2$ 。 U = 4 个移动设备，随机放置在该覆盖区域内。无人机在同一坐标 $c(1) = c(N) =(0,0)$ 处开始和结束飞行，无人机总飞行时间为 40s ，总重量为 6kg 。无人机的 MEC 服务器的最大计算能力为 1GHz ，移动设备的最大计算能力在 [0.1,0.72]MHz 之间随机产生。移动设备计算任务的输入数据大小和执行 1 位输入数据所需的 CPU 周期分别在 $[0.4 × 10^5, 1 × 10^5]$ 位和 [5,25] 周期之间随机生成。那么，移动设备的可容忍延迟在 [5,20]s 之间。最大可用带宽30MHz，加性高斯噪声功率−174dbm /Hz。移动设备的最大发射功率为100 mW。

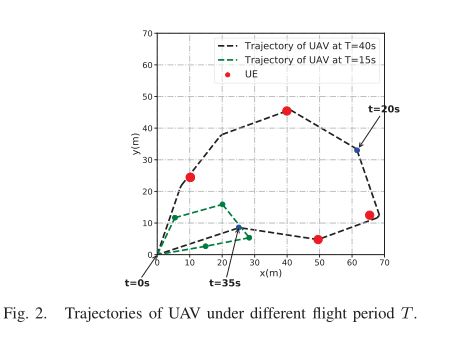
图 2 显示了本文提出的 BSUM 算法下的无人机最优轨迹，将无人机总飞行时间 T = 40 s 等分成 13 个时隙，每个时隙飞行时间为 5s 。然后，将无人机的飞行时间调整到 15s ，在该算法下找到最优无人机轨迹。因此，从图 2 中我们可以看出，当飞行时间足够大时，无人机会飞近移动设备。

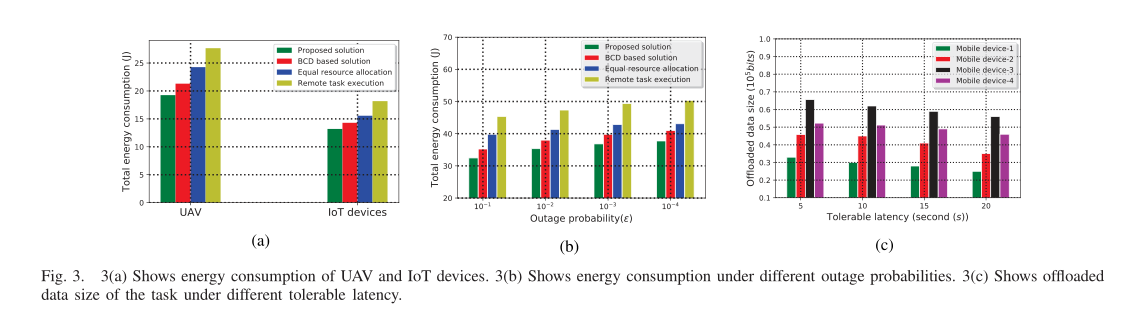
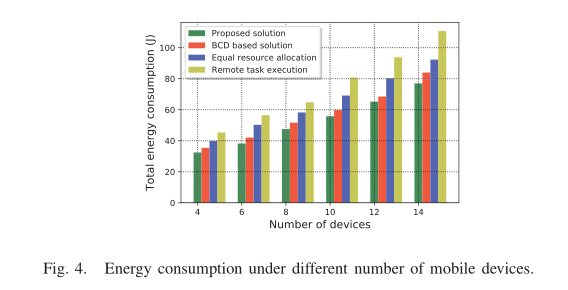
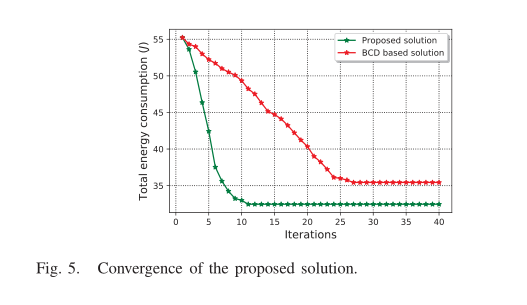
在图 3a 中，我们展示了无人机飞行能量、边缘计算能量等总能耗，以及物联网设备上行传输能量和本地计算能量等总能耗。此外，我们还将我们提出的算法与块坐标下降 (Block Coordinate Descent, BCD) 方法和其他两种基线方案进行了比较: 1) 资源均衡分配，将部署在无人机上的 MEC 服务器的无线带宽和计算能力平均分配给所有设备; 2) 任务远程执行，移动设备将所有的计算任务卸载到无人机上的服务器，并远程执行任务。从图中可以看出，在我们提出的算法下，无人机和物联网设备的能耗比其他方案都要低。图 3b 为可容忍停电概率与能耗的关系。在这种情况下，当设备中断概率较高时，就会增加设备的传输功率，以达到所需的高数据速率。因此，当我们收紧中断概率时，我们观察到能量消耗的增加，如图 3b 所示。图 3c 为可容忍延迟对每个移动设备向部署在无人机上的 MEC 服务器卸载数据大小的影响。从图 3c 中可以看出，当可容忍延迟增加时，每个移动设备向 MEC 服务器传输的数据更少，即它有足够的时间在本地执行计算任务。但缺点是会增加设备的能耗。图 4 描述了不同数量移动设备时网络的总能耗(即移动设备和无人机的能耗)。从图 4 可以看出，我们提出的方案优于其他基线方案。随着用户数量的增加，我们提出的方案与其他方案的性能差距越来越大。因此，当系统中存在大量用户时，我们提出的方案更有效。最后，图 5 显示了我们提出的解决方案在几个迭代内收敛到次优解决方案。此外，我们还从图中注意到，我们提出的解决方案收敛速度比BCD方法快。

5.总结

在这篇文章中，我们研究了无人机辅助移动边缘计算系统中节能无人机轨迹优化、资源分配和任务卸载问题，我们的目标不仅是最小化移动设备的能源消耗，而且是无人机的推进和计算能力。我们已经证明了所研究的问题呈现非凸结构，因此，用传统的凸优化技术来解决它是具有挑战性的。为了解决这一问题，我们引入了 BSUM 算法，它是解决非凸非光滑问题的有力工具。最后，我们给出了数值结果，以显示所提出的解决方法的效率，其中很明显，我们提出的算法优于其他基线算法。