无人机辅助移动边缘计算的计算卸载优化:一种深度确定性策略梯度方法
摘要:无人机(UAV)可以在无线系统中发挥重要作用,因为它可以灵活地部署,帮助提高通信的覆盖和质量。本文研究了一种无人机辅助的移动边缘计算(MEC)系统,在该系统中,无人机配备了计算资源,可以为附近的用户设备提供卸载服务。终端将部分计算任务卸载给无人机,其余计算任务在终端本地执行。在离散变量和能量消耗约束下,通过联合优化用户调度、任务卸载率、无人机飞行角度和飞行速度,以最小化最大处理延迟为目标。考虑到该问题中高维状态空间和连续动作空间的非凸性,提出了一种基于深度确定性策略梯度(DDPG)的强化学习算法。利用该算法,我们可以在不可控的动态环境下得到最优的计算卸载策略。实验结果表明,该算法能够快速收敛到最优解。与此同时,我们的算法在处理延迟方面比基线算法(如深度Q网络(DQN))有很大的提高。
1 介绍
1.1 动机
随着5G技术的发展,运行在用户设备(User Equipment,UE)上的计算密集型应用,如网络游戏、VR/AR和远程医疗,将变得更加繁荣和流行。这些移动应用通常需要大量的计算资源和高能耗。然而,目前的终端普遍存在计算资源和电池容量的限制。移动云计算(MCC)是为了提高终端的计算和存储能力,并通过移动网络将计算转移到云端,从而降低终端的能耗而出现的。但由于云服务器与终端之间的空间距离较远,导致传输延迟较大,影响用户体验。为了减少回程链路延迟,移动计算最近转向了一种新的计算范式,即移动边缘计算(Mobile Edge Computing, MEC)。MEC可以将云计算资源和业务迁移到离终端更近的地方,从而有效降低通信延迟和能耗。
早期对 MEC 的研究主要集中于提高 MEC 系统的性能,在 MEC 系统中,计算服务由固定位置的基站提供。例如, Tran 等人在多用户多服务器的 MEC 系统中提出了一种用于优化资源分配的凸优化方法和一种用于任务卸载的低复杂度启发式算法。Zhao等人的目标是在云辅助的 MEC 系统中通过协同计算卸载和资源分配优化(CCORAO)方案实现系统效用最大化。为了降低基于多用户 MIMO 的 MEC 系统的计算成本,Chen等人提出了一种深度强化学习方法来动态生成连续功率分配策略。但是,固定基础设施提供的MEC服务在通信设施稀疏或发生突发性自然灾害的情况下无法有效工作。
近年来,无人机(Unmanned Aerial Vehicle,简称UAV)以其高机动性、部署灵活等特点受到了广泛的关注。他们研究了无人机辅助MEC系统中的资源分配或路径规划。针对无人机辅助MEC系统中终端间的处理延迟,Hu等开发了一种基于惩罚对偶分解优化框架的算法,通过联合优化无人机轨迹、计算卸载和用户调度。刁等设计了一种基于节能的联合无人机轨迹和任务数据分配优化算法。Cheng等人提出了一种新的边缘计算体系结构——无人机辅助空对地综合网络(SAGIN),并设计了一种基于行为者批评的强化学习(RL)算法用于资源分配和任务调度。在基于无人机的MEC系统中,考虑到状态空间的维数灾难,Li等人采用了RL算法来提高UEs任务迁移的吞吐量。Xiong等提出了一种通过联合优化卸载决策、钻头分配和无人机轨迹来降低能耗的优化算法。Selim et al.提出使用设备到设备(D2D)作为无人机- mec系统辅助通信和计算卸载的附加选项。在广泛的研究和应用中,无人机辅助的MEC系统仍然面临着许多挑战,例如, UE 计算能力的限制和环境障碍物(如树木或建筑物)的阻塞严重影响了系统性能,特别是在城市地区。因此,自适应链路选择和任务卸载问题在无人机辅助的 MEC 系统中是非常重要的。
1.2 新颖性与贡献
在本文中,我们考虑了一个由安装有纳米服务器的无人机和多个终端组成的MEC系统,其中通信条件是动态和时变的。与基于深度Q网络(DQN)的离散动作空间算法不同,本文设计了一种新的基于深度确定性策略梯度(DDPG)的计算卸载算法,该算法能够有效支持任务卸载和无人机机动的连续动作空间。本文的主要贡献如下:
考虑时变信道状态下的分时段无人机辅助MEC系统,联合优化用户调度、无人机机动性和资源分配,将非凸计算卸载问题定义为马尔可夫决策过程(MDP)问题,以最小化处理延迟。
当我们考虑MDP模型时,系统状态的复杂性非常高。此外,计算卸载的决策需要对连续动作空间的支持。因此,我们提出了一种新的基于DDPG的计算卸载方法。DDPG是一种先进的强化学习算法,它利用行动者网络生成独特的动作,利用批评网络逼近q值动作函数。本文采用 DDPG 算法对无人机辅助 MEC 系统中的用户调度、无人机机动性和资源分配进行优化。
DDPG算法是在 TensorFlow 平台上实现的。不同系统参数下的仿真结果验证了该算法的有效性。在不同的通信条件下,与其他基线算法相比,我们的算法总能取得最好的性能。
本文的其余部分组织如下。第二节介绍了无人机辅助 MEC 系统的系统模型,以及优化问题。第3节简要介绍了深度强化学习的初步研究。第四节提出了基于 DDPG 的计算卸载算法。第 5 节给出了我们提出的算法的仿真结果,并与其他基线算法进行了比较。最后,第六节总结了本工作。
2 系统模型
我们考虑了一种无人机辅助的MEC系统,该系统由UE和配备纳米MEC服务器的无人机组成。整个系统运行在离散时间内,时隙长度相等。对所有终端提供通信和计算服务,但一次只能对一个终端。由于计算能力的限制,终端必须通过无线网络将部分计算任务转移到无人机的MEC服务器上。
2.1 通信模型
无人机以时间划分方式向所有终端提供计算服务,将整个通信周期 T 划分为 I 个时隙。我们假设 UEs 在该区域内以低速随机移动。在每个时间段,无人机在固定位置悬停,然后与其中一个终端建立通信。终端将部分计算任务卸载到服务器上后,剩余的计算任务将在本地执行。在三维笛卡尔坐标系下,无人机保持在固定高度 H 飞行,无人机的起始坐标 q(i)=[x(i),y(i)]T∈R(2×1) 和结束坐标q(i+1)=[x(i+1),y(i+1)]T∈R(2×1) 在时隙 i∈{1,2,⋯,I} 。UE坐标 k∈{1,2,⋯,K} 是 pk(i)=[xk(i),yk(i)]T∈R(2×1) 。无人机与UE k之间的视距链路的信道增益可以表示为:
gk(i)=α0dk−2(i)=∣∣q(i+1)−pk(i)∣∣2+H2α0
式中,α0 为参考距离 d=1m 处的信道增益,dk(i) 为无人机与 k 之间的欧氏距离。由于障碍物的遮挡,无线传输速率可表示为:
rk(i)=Blog2(1+σ2+fk(i)PNLOSPupgk(i))
B 表示通信带宽, Pup 表示终端在上传链路的传输功率,σ2 表示噪声功率,PNLOS 表示传输损耗, fk(i) 表示在时刻 i , UAV 与 UE k 之间是否有阻塞的指示器(即0表示无堵塞,1表示堵塞)。
2.2 计算模型
在我们的MEC系统中,在每个时隙中对终端的任务使用了部分卸载策略。设 Rk(i)∈[0,1] 表示卸载到服务器的任务的比例, (1−Rk(i)) 表示在终端本地执行的剩余任务。那么,UE k在第 i 个时隙的本地执行延迟可以表示为:
tlocal,k(i)=fUE(1−Rk(i))Dk(i)s
其中, Dk(i)为UE k的计算任务大小, s 为 UE 处理每个单位字节所需的CPU周期, fUE 为 UE 的计算能力。在第一个时间段,无人机从位置 q(i) 飞行到新的悬停位置
q(i+1)=[x(i)+v(i)tflycosβ(i),y(i)+v(i)tflysinβ(i)]T
其中,速度为 v(i)∈[0,vmax] 以及角度 β(i)∈[0,2π] 。本次飞行所消耗的能量可以表示为:
Efly(i)=ϕ∣∣v(i)∣∣2
其中 ϕ=0.5MUAVtfly , M 与无人机的有效载荷相关,tfly 为固定飞行时间。在MEC系统中,服务器提供的计算结果的大小通常非常小,可以忽略不计。因此,这里不考虑下行链路的传输延迟。MEC服务器的处理延迟可分为两部分。一部分是传输时延,可以表示为:
ttr,k(i)=rk(i)Rk(i)Dk(i)
另一部分是在MEC服务器上计算产生的延迟,可以表示为:
tUAV,k(i)=fUAVRk(i)Dk(i)s
其中 fUAV 为服务器CPU计算频率。相应的,在 i 时间段将计算任务卸载给服务器所消耗的能量也可以分为两部分,一部分用于传输,一部分用于计算。在MEC服务器上进行计算时,其功耗可表示为:
PUAV,k(i)=κfUAV3
则 MEC 服务器在第 i 时刻的能耗为:
EUAV,k(i)=PUAV,k(i)tUAV,k(i)=κfUAV2Rk(i)Dk(i)s
2.3 问题公式化
在此基础上,提出了无人机辅助MEC系统的优化问题。为了确保有限的计算资源的有效利用,我们的目标是通过联合优化用户调度、无人机机动性和系统中的资源分配,使所有终端的最大处理延迟最小化。具体而言,优化问题可以表示为:
{αk(i),q(i+1),Rk(i)}mini=1∑Ik=1∑Kαk(i)max{tlocal,k(i),tUAV,k(i)+ttr,k(i)} s.t. αk(i)∈{0,1},∀i∈{1,2,…,I},k∈{1,2,…,K},k=1∑Kαk(i)=1,∀i,0≤Rk(i)≤1,∀i,k,q(i)∈{(x(i),y(i))∣x(i)∈[0,L],y∈[0,W]},∀i,p(i)∈{(xk(i),yk(i))∣xk(i)∈[0,L],yk∈[0,W]},∀i,k,fk(i)∈{0,1},∀i,k,i=1∑I(Efly,k(i)+EUAV,k(i))≤Eb,∀k,i=1∑Ik=1∑Kαk(i)Dk(i)=D
其中,等式 (9b)和等式 (9c)保证在第 i 个时间段只有一个用户被调度到计算中。等式 (9d)为计算任务卸载率的取值范围。约束(9e)和(9f)表示 UE 和 UAV 只能在给定区域内移动。约束(9g)表示无人机与终端之间的无线信道在 i 时隙被堵塞。约束(9h)保证无人机在所有时隙飞行和计算的能耗不超过最大电池容量。约束(9i)指定整个时间段内需要完成的所有计算任务。
3 基于DDPG的计算卸载优化
在本节中,我们首先介绍 MDP 、 Q-Learning 、 DQN 和 DDPG 这些重要的新兴 RL 技术的基本知识。然后,讨论了如何利用 DDPG 来训练无人机辅助MEC系统的高效计算卸载策略。详细地定义了状态空间、动作空间和奖励函数,描述了数据预处理的状态归一化,并举例说明了训练算法和测试算法的过程。
3.1 RL介绍
3.1.1 MDP
MDP 是描述离散时间随机控制过程的数学框架,在该过程中,结果是部分随机的,并且处于主体或决策者的控制下。它正式地描述了一个环境,它是完全可观察到的强化学习。通常, MDP 可以定义为一个元组 (S,A,p(.,.),r) ,S 是状态空间, A 是动作空间,p(si+1∣si,ai) 是执行动作 ai∈A 从当前状态 si∈S 到下一状态 si+1∈S 的转移概率,同时 $r: \mathcal S \times \mathcal{A} \rightarrow \mathcal R $是即时/即时奖励功能。我们表示 $\pi : \mathcal S \rightarrow \mathcal P(\mathcal A) $ 作为一个“策略”,它是从一个状态映射到一个动作。MDP的目标是找到一个最优的政策,可以最大化预期的累积回报:
Ri=l=i∑∞γl−irl
其中, γ∈[0,1] 是折扣因子, rl=r(sl,al) 是第 l 个时间段的即时奖励。在策略 π 下,状态 si 的预期折现收益定义为状态值函数,即
Vπ(si)=Eπ[Ri∣si]
同样,在策略 π 下,si 状态下采取行动 ai后的预期折现收益定义为一个行动值函数,即:
Qπ(si)=Eπ[Ri∣si,ai]
根据 Bellman 方程,状态值函数和动作值函数的递归关系分别表示为:
Vπ(si)=Eπ[r(si,ai)+γVπ(si+1)]Qπ(si,ai)=Eπ[r(si,ai)+γQπ(si+1,ai+1)]
既然我们的目标是找到最优的政策 π∗ 时,可通过最优值函数求出各状态下的最优动作。最优状态值函数可以表示为:
V∗(si)=ai∈AmaxEπ[r(si,ai)+γVπ(si+1)].
最优行为值函数也遵循最优策略 π∗ ,我们可以写出 用 Q∗ 使用 V∗ 表示如下:
Q∗(si,ai)=Eπ[r(si,ai)+γV∗(si+1)]
3.1.2 Q-learning
RL是机器学习的一个重要分支,agent通过与控制环境交互,使其达到最优状态,从而获得最大的收益。虽然RL常用于解决 MDPs 的优化问题,但潜在传播概率 p(si+1∣si,ai) 是未知的,甚至是不稳定的。在RL中,agent试图通过与控制环境的交互,并通过之前的经验调整自己的行为来获得最大的回报。Q-learning 是RL中一种流行而有效的方法,它是一种 off-policy 时差(TD)控制算法。状态-行为函数即最优Q函数的Bellman最优方程可以表示为:
Q∗(si,ai)=Eπ[r(si,ai)+γai+1maxQ∗(si+1,ai+1)]
通过迭代过程可以找到Q函数的最优值。agent从经验元组 (si,ai,ri,si+1) 学习,Q函数可在第 i 步时间更新如下:
Q(si,ai)←Q(si,ai)+α[r(si,ai)+γai+1maxQ(si+1,ai+1)−Q(si,ai)]
其中, α 为学习率, r(si,ai)+γmaxai+1Q(si+1,ai+1) 为预测的Q值, Q(si,ai) 是当前Q值。预测Q值和当前Q值之间的差就是TD误差。当选择合适的学习速率时,Q学习算法收敛。
3.1.3 DQN
Q-learning 算法通过维护一个查询表更新状态动作空间中各项的Q值,适用于状态动作空间较小的情况。考虑到实际系统模型的复杂性,这些空间通常是非常大的。原因是大量状态很少被访问,对应的 Q 值很少更新,导致Q函数的收敛时间较长。 DQN 通过将深度神经网络(DNNs)与Q-learning算法相结合,解决了Q-learning算法的不足。DQN的核心思想是利用 θ 参数化的DNN来求得近似的Q值 Q(s,a) 代替 Q 表,即 Q(s,a∣θ)≈Q∗(s,a) 。
但是使用 DNN 的 RL 算法的稳定性不能得到保证。为了解决这个问题,采用了两种机制。第一个是体验重放(experience replay)。在每个时间步 i 中,agent的交互经验元组 (si,ai,ri,si+1) 存储在经验重放缓冲区,即经验池 Bm。然后,从经验池中随机选取少量样本,即小批量,对深度神经网络的参数进行训练,而不是直接使用连续样本进行训练。第二种稳定方法是使用一个目标网络,它最初包含了设定策略的网络的权值,但在固定的时间步长内保持冻结状态。目标Q网络更新缓慢,但主Q网络更新频繁。这样大大降低了目标与估计Q值之间的相关性,使得算法更加稳定。
在每次迭代中,通过最小化损失函数 L(θ),将深度 Q 函数训练到目标值。损失函数可以写成:
L(θ)=E[(y−Q(s,a∣θ))2]
其中目标值 y 表示为 y=r+γmaxa′Q(s′,a′∣θi−) 。在 Q-learning 中,权值 θi−=θi−1 ,而在深度q学习 θi−=θ1−X ,即目标网络权值每 X 个时间步更新一次。
3.1.4 DDPG
DQN算法虽然可以解决高维状态空间的问题,但仍然不能处理连续的动作空间。DDPG算法是一种基于DNN的无模型的off-policy actor - critic算法,可以学习连续动作空间中的策略。该算法由策略函数和q值函数组成。策略函数扮演一个参与者来生成动作。q值函数作为一个批评家,评价参与者的表现,并指导参与者的后续行动。
如图 1 所示,DDPG使用两个不同的 DNNs 来逼近actor网络 μ(s∣θμ) (即policy function)和critic 网络 Q(s,a∣θQ) (即Q-value funtion)。另外,行动者网络和批评网络都包含一个与它们结构相同的目标网络:使用参数 θμ′ 的行动者目标网络 μ′ ,使用参数 θQ′ 的批评目标网络 Q′。与 DQN 相似,批评家网络 Q(s,a∣θQ) 可以更新如下:
L(θQ)=Eμ′[(yi−Q(si,ai∣θQ))2]
其中,
yi=ri+γQ(si+1,μ(si+1)∣θQ)
正如Silver等人所证明的,策略梯度可以用链式法则更新,
∇θμJ≈Eμ′[∇θμQ(s,a∣θQ)∣∣∣s=si,a=μ(si∣θμ)]=Eμ′[∇aQ(s,a∣θQ)∣∣∣s=si,a=μ(si∣θμ)∇θμμ(s∣θμ)∣∣∣∣s=si].
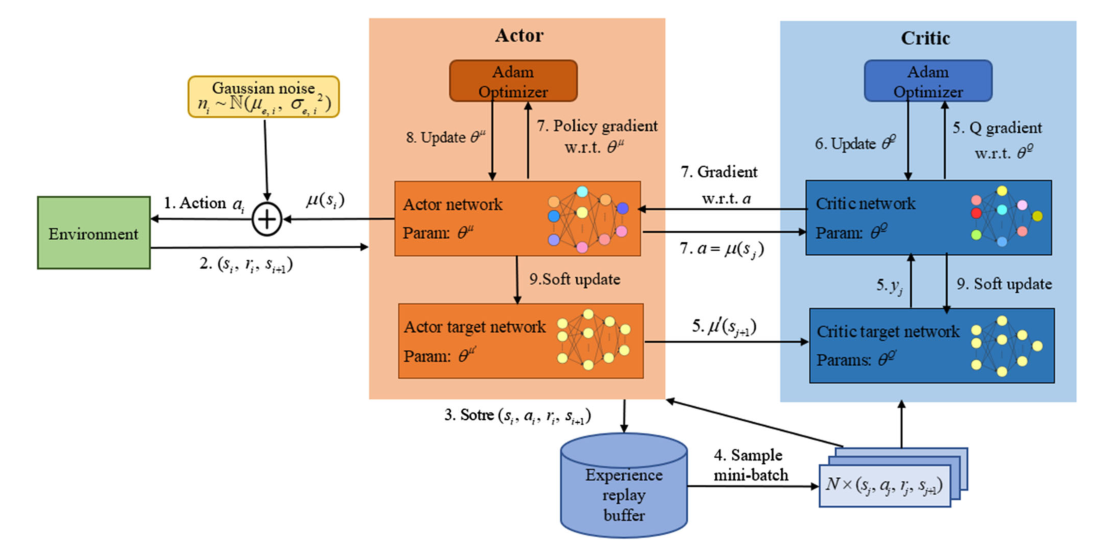
DDPG 算法的整个训练过程可以总结如下:首先,演员网络 μ 在上一个训练步骤之后输出 μ(si)。为了提供充分的状态空间探索,我们需要在探索和开发之间取得平衡。实际上,我们可以将 DDPG 的探索与学习过程分开来看待,因为 DDPG 是一种 off-policy 算法。因此,我们通过添加行为噪声 ni 来构造动作空间,以获得动作 ai=μ(si)+ni ,其中 ni 服从高斯分布 ni∼N(μe,σe,i2) , μe 为平均值, σe,i 是标准差。在环境中表演 at 后,agent 可以观察到下一个状态 si+1 和即时奖励 rt。然后将元组 (si,ai,ri,si+1) 存储在体验回放缓冲区中。之后,算法随机选择N个元组 (sj,aj,rj,sj+1) 在缓冲区中组成一个小批量,并将其输入演员网络和评论家网络。使用小批处理,演员目标网络 μ′ 将行为 μ′(sj+1) 输出到评论目标网络 Q′。利用 minibatch 和 μ′(sj+1) ,批评家网络可以根据 yi=ri+γQ(si+1,μ(si+1)∣θQ) 计出目标值 yj。
为了使损失函数最小化,批评家网络Q将由给定的优化器(如Adam optimizer)进行更新。然后,演员网络 μ 将小批量动作 a=μ(sj) 发送给评论网络,以实现动作a的梯度 ∇aQ(s,a∣θQ)∣∣∣s=sj,a=μ(sj) 。参数 ∇θμμ(s∣θμ)∣s=sj 可以由它自己的优化器导出。使用这两个梯度,参与者网络可以用以下近似更新:
∇θuJ≈N1j∑[∇aQ(s,a∣θQ)∣∣∣s=sj,a=μ(sj∣θμ)∇θμμ(s∣θμ)∣∣∣∣s=sj].
最后,DDPG agent使用小常数 τ 柔化更新批评家目标网络和行动者目标网络:
θQ′←θQ+(1−τ)θQ′θμ′←θμ+(1−τ)θμ′
4 DDPG-based算法
4.1 状态空间
在无人机辅助的MEC系统中,状态空间由 k 个用户、一个无人机及其环境共同确定。时间槽 i 处的系统状态可定义为:
si=(Ebattery (i),q(i),p1(i),…,pK(i),Dremain (i),D1(i),…,DK(i),f1(i),…,fK(i)),
式中, Ebattery (i) 为 i 时刻无人机电池剩余能量, q(i) 为无人机位置信息, pK(i) 为无人机服务的UE k的位置信息, Dremain(i) 为整个时间段系统需要完成的剩余任务大小, DK(i) 为UE k在 i 时刻随机生成的任务大小, fK(i) 表示UE k的信号是否被障碍物阻挡。特别是当 i=1 , Ebattery (i)=Eb 和 Dremain(i)=D 。
4.2 行动空间
agent根据系统当前状态和所观察的环境,选择待服务的动作包括 i 时刻被服务的UE k′ 、无人机飞行角度、无人机飞行速度、任务卸载比等,动作 ai 表示为:
ai=(k(i),β(i),v(i),Rk(i))
值得注意的是,DDPG中的演员网络输出连续的动作。被 agent 选择的动作变量 UE k(i)∈[0,K] 需要进行离散化,即如果 k(i)=0 ,则 k′=1 ;如果 k(i)=0 ,则 k′=⌈k(i)⌉, 其中 ⌈⋅⌉ 为向上取整操作。在一个连续动作空间内,可以精确优化无人机的飞行角度、飞行速度和任务卸载比,即 β(i)∈[0,2π], v(i)∈[0,vmax] ,以及 Rk(i)∈[0,1] 。对以上四个变量进行联合优化,使系统成本最小。
4.3 奖励函数
agent 的行为是基于奖励的,选择合适的奖励函数对 DDPG 框架的性能起着至关重要的作用。我们的目标是通过最小化问题 (9) 中定义的处理延迟来实现回报最大化,如下所示:
ri=r(si,ai)=−τdelay (i)
其中,时间槽 i 的处理延迟为
τdelay (i)=k=1∑Kαk(i)max{tlocal ,k(i),tUAV,k(i)+ttr,k(i)}
,并且如果 k=k′ ,则 αk(i)=1 ;否则 αk(i)=0 。通过DDPG算法,可以找到使Q值最大化的动作。系统的长期平均报酬可以用 Bellman 方程表示为:
Qμ(si,ai)=Eμ[r(si,ai)+γQμ(si+1,μ(si+1))]
4.4 状态标准化
在 DNN 的训练过程中,输入在每一层的分布会随着前一层参数的变化而变化,这需要较低的学习速率和细致的参数初始化,从而减慢了训练的速度。Ioffe 和 Szegedy 提出了一种批处理归一化机制,该机制允许训练使用更高的学习率,并且对初始化不那么小心。我们提出了一种状态归一化算法对观测状态进行预处理,从而更有效地训练 DNN 。值得注意的是,与Qiu的状态归一化算法不同,本文算法将每个变量的最大值与最小值之差作为尺度因子。所提出的状态归一化算法可以很好地解决输入变量的大小差异问题。
在我们的工作中,变量 Ebattery (i),q(i),p1(i),…,pK(i),Dremain (i),D1(i),…,DK−1(i) 和 DK−1(i) 在状态集中处于不同的序列,这可能导致在训练中出现问题。如算法 1 所示,通过状态归一化对这些变量进行归一化,以防止出现这种问题。在状态归一化算法中,我们使用了五个尺度因子。每个因素可以解释如下。利用缩放因子 γb 来缩小无人机电池容量。由于 UAV 和 UE 具有相同的 x 和 y 坐标范围,我们使用 γx 和 γy 分别缩小UAV和UE的x和y坐标。我们使用 γDrm 来缩小整个时间段内剩余的任务,使用 γDUE 来缩小时间段 i 内每个终端的任务大小。

4.5 训练与测试
对基于 DDPG 的计算卸载算法的学习和评估分为训练和测试两个阶段。基于DDPG的计算卸载训练算法如算法 2 所示。在训练过程中,对训练行为策略的批评家网络参数和演员网络参数进行迭代更新。算法 3 描述了计算卸载测试过程,采用了算法 2 中训练好的演员网络 θμ 。需要注意的是,由于演员网络是用归一化状态进行训练的,所以在测试过程中,我们还需要对输入状态进行预处理。


5 结果与分析
在本节中,我们通过数值模拟来说明提出的基于 DDPG 的无人机辅助 MEC 系统计算卸载框架。首先,介绍了仿真参数的设置。然后,对基于 DDPG 的框架在不同场景下的性能进行了验证,并与其他基线方案进行了比较。
5.1 仿真设置
在无人机辅助的 MEC 系统中,我们考虑一个 K=4 UEs 随机分布在 L×W=100×100m2 的2维平面,假设无人机在固定高度 H=100m 飞行。根据[26]的定义,无人机的总质量为 MUAV=9.65kg 。整个时间段 T=400s分为 I = 40 个时隙。参考[9],无人机最大飞行速度vmax=50m/s,无人机在每个时隙的飞行时间 tfly=1s 。在参考距离为1米时,通道功率增益被设置为 α0=−50dB 。设置传输带宽为 B=1MHz。假设没有信号遮挡下,接收机的噪声功率为 σ2=−100dBm 。如果信号在无人机与UE k之间传输过程中被阻塞,即信号为 fk(i)=1 。
渗透损失为 PNLOS=20dB 。我们假设 UEs 的传输功率为 Pup=0.1W, UAV电池容量 Eb=500kJ 和所需CPU周期/位 s=1000 周期/位。UE 和 MEC 服务器的计算能力分别设置为 fUE=0.6GHz 和 fUAV=1.2GHz。将所提出的状态归一化算法中的比例因子分别设置为 γb=5×105,γx=100,γy=100,γDrm=1.05×108,γDUE=2.62×106 。除另有说明外,具体仿真参数如表1所示。在我们的实验中,使用算法 3 在相同设置下多次运行获得的平均奖励来进行性能比较。
为作比较,现将四种基线方法说明如下:
- 将所有任务卸载到无人机(仅卸载):在每个时间段,无人机将在区域中心的固定位置向终端提供计算服务。UE 将所有的计算任务都交给无人机上的 MEC 服务器处理。
- 全本地执行(Local-only):在不借助无人机的情况下,终端的所有计算任务都在本地执行。
- 基于Actor Critical 的计算卸载算法 (AC):为了评价本文提出的基于 DDPG 的计算卸载算法的性能,在计算卸载问题上还实现了基于连续动作空间的 RL 算法 AC 。为了与 DDPG 进行比较, AC 还采用了状态归一化。
- 基于DQN的计算卸载算法(DQN):将传统的基于离散动作空间的 DQN 算法与提出的基于 DDPG 的算法进行比较。在无人机飞行过程中,角度水平被定义为 B={0,π/5,…,2π} ,速度级别表示为 V={0,vmax/10,…,vmax} 和卸载比级别可设置为 O={0,0.1,…,1.0} 。为了与DDPG和AC进行比较,DQN还采用了状态归一化。
5.2 仿真结果与讨论
5.2.1 参数分析
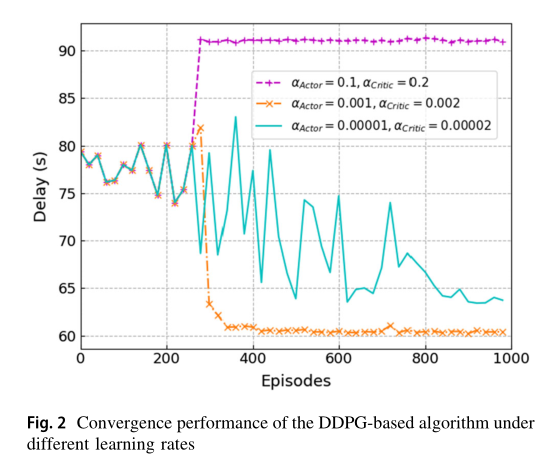
我们首先进行了一系列的实验,以确定最优值的重要超参数用于算法比较。本文算法在不同学习速率下的收敛性能如图 2 所示。我们假设评论网络和演员网络的学习速度是不同的。首先,我们可以清楚地看到,当 αActor =0.1,αCritic =0.2 或 αActor =0.001,αCritic =0.002 时,提出的算法可以收敛。但当 αActor =0.1,αCritic =0.2 时,算法收敛到局部最优解。究其原因,大的学习率将使批评家网络和演员网络都有一个大的更新步骤。其次,我们可以发现当学习速率很小时,即 αActor =0.00001,αCritic =0.00002 时,算法不能收敛。这是因为较低的学习率会导致dnn的更新速度较慢,需要更多的迭代片段来收敛。因此,actor网络和critic网络的最佳学习率分别为 αActor =0.001,αCritic =0.002 。
在图 3 中,我们比较了不同折扣因子 γ 对算法收敛性能的影响。结果表明,当折扣因子 γ=0.001时,训练后的计算卸载策略性能最佳。原因是不同时期的环境差异很大,所以整个时间段的数据不能完全代表长期的行为。 γ 越大,说明 Q 表将整个时间段收集的数据视为长期数据,导致不同时间段的泛化能力较差。因此,适当的 γ 值将提高我们训练后的策略的最终性能,在接下来的实验中,我们将折扣因子 γ 设置为0.001。
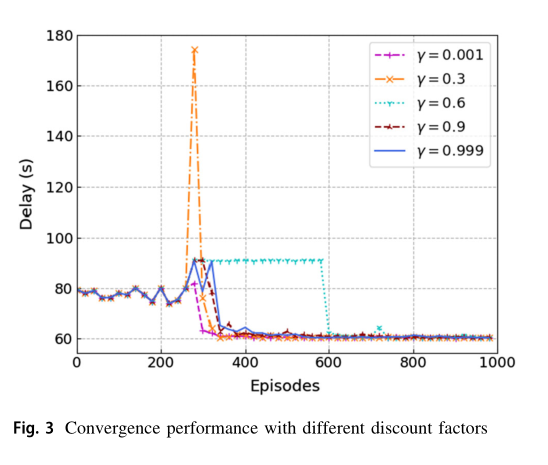
图 4 显示了在不同探测参数 σe 下,本文算法在处理延迟方面的性能比较。该探测参数对算法的收敛性能影响很大。当算法收敛于 σe=0.1 时,最佳延迟在63秒上下波动。 σe 值越大,随机噪声分布空间就越大,这使得 agent 可以探索更大的空间范围。当 σe=0.001 时,算法在850次迭代时性能下降, σe 较小,算法陷入局部最优解。因此,需要进行大量的实验才能获得无人机辅助场景下合适的探索设置。因此,为了在接下来的实验中获得更好的性能,我们选择 σe=0.01 。
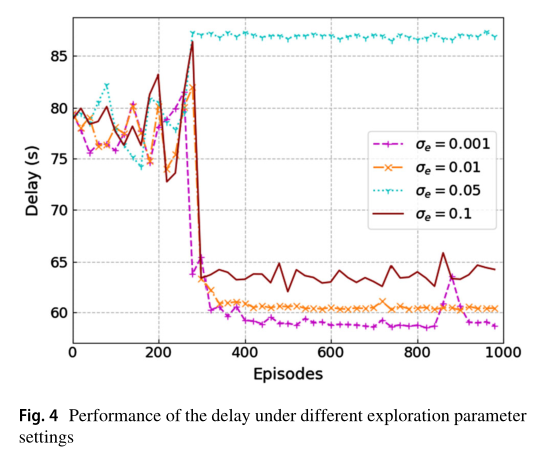
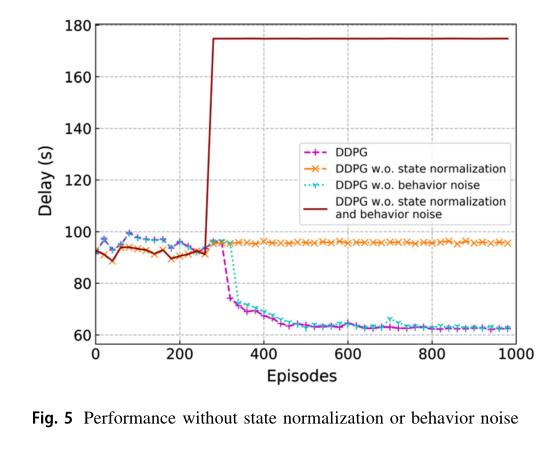
图 5 显示了不使用状态归一化和行为噪声的训练策略对 DDPG 训练算法的影响。一方面,如果在没有行为噪声的情况下训练 DDPG 算法,算法的收敛速度会变慢。另一方面,如果不进行状态归一化训练,即在状态归一化中不引入尺度因子,训练算法将失效。这是因为在没有状态归一化策略的情况下,Ebattery (i)、 Dremain (i) 和 Dk(i) 的值都太大,导致 DNNs 的随机初始化输出更大的值。因此,如果在 DDPG 算法中不采用我们提出的状态归一化策略,该算法最终会变成贪婪算法。
5.2.2 性能比较
图 6 显示了不同算法之间的性能比较。在图 6a 中,我们对 RL算法的 DNNs 进行了总计1000次迭代的训练。从图中可以看出,随着迭代次数的增加, AC 算法不能收敛,而 DQN 和 DDPG 算法都可以收敛。这是因为 AC 算法存在着行动者网络和批评网络同时更新的问题。行动者网络的行为选择依赖于评论网络的价值功能,但评论网络本身难以收敛。因此,AC算法在某些情况下可能不收敛。相比之下, DQN 和 DDPG均受益于评价网络和目标网络的双网络结构,可用于切断训练数据之间的相关性,从而找到最优的行动策略。利用算法收敛后的延迟结果,比较不同任务大小设置下的算法,结果如图 6b 所示。在图 6b 中,对于相同的任务大小, DDPG 算法的时延在五种算法中始终是最低的。由于探索了离散的动作空间和可用动作之间的不可忽略空间, DQN 无法准确地找到最优卸载策略。而 DDPG 算法则探索一个连续的动作空间,并采取一个精确的动作,最终获得最优策略,显著减少了延迟。此外, DQN 算法的收敛速度远高于 DDPG 算法。 Offload-only 和 Local-only 两种算法不能充分利用整个系统的计算资源。因此,对于相同的任务大小, DDPG 算法的处理延迟明显低于 Offload-only 和 Local-only 算法。此外,随着任务大小的增大, DDPG 算法优化后的处理延迟增加速度明显慢于 Offload-only 和 Local-only 算法,表明了该算法的优势。
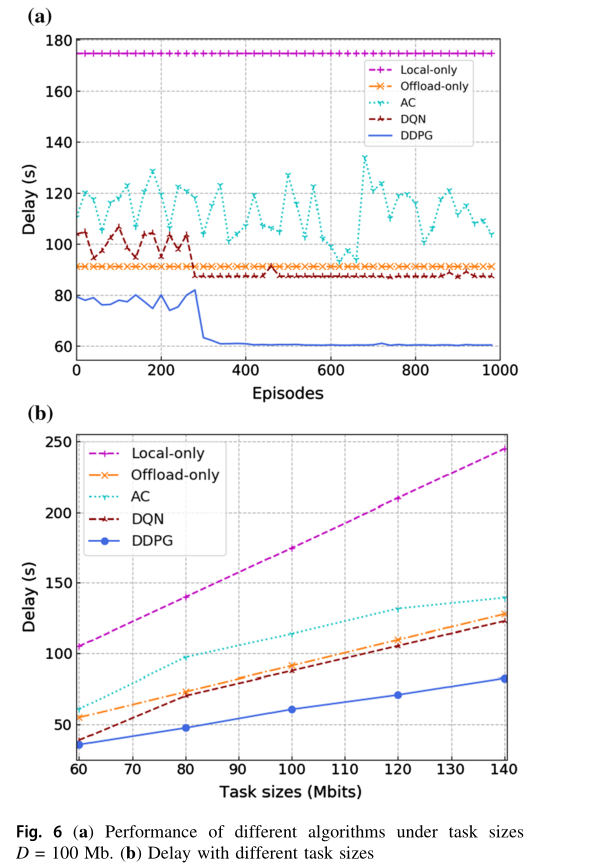
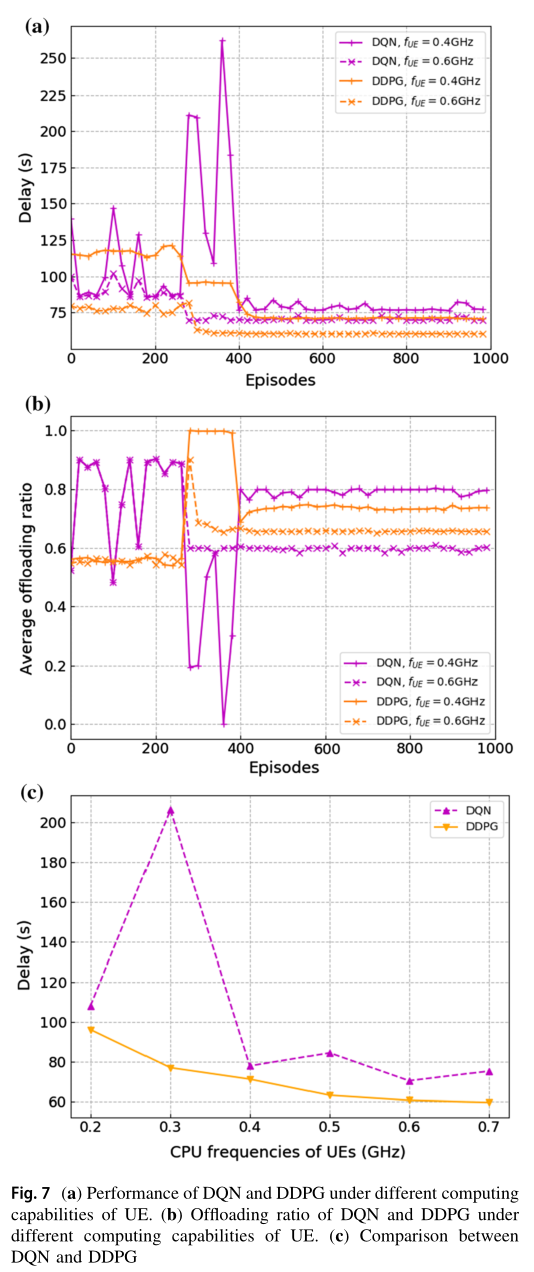
图 7a 和图 b 显示了同一组实验在延迟和卸载比方面的性能。图 7a 显示了不同 UE 计算能力下 DQN 方案和 DDPG 方案的收敛性能。本文提出的方案之所以没有与 AC 方案进行比较,是因为 AC 方案仍然不收敛。我们可以发现,当 UE 的计算能力较小时,即 fUE=0.4GHz 时,两种优化方案优化后的处理延迟要高于 $$f_{UE}=0.6 GHz$$ 时的处理延迟。另一方面,从图 7b 中可以看出,当 UE 的计算能力较大时,系统的平均卸载率较小,因此 UE 更倾向于在本地执行任务。 UE 的计算能力越小,同时系统的数据处理速度越慢,导致本地执行和卸载之间的最大延迟越大。图 7c 为本文方案与 DQN 方案在不同 CPU 频率条件下优化后的时延比较。由图 7c 可以看出,在不同 UE 计算能力下,与 DQN 方案相比,本文提出的 DDPG 方案具有更低的延迟。这是因为 DDPG 方案可以输出多个连续的动作,而不是 DQN 中有限的离散动作集。因此, DDPG 可以找到一个精确的、对连续动作控制系统延迟影响较大的因子,即卸载比。
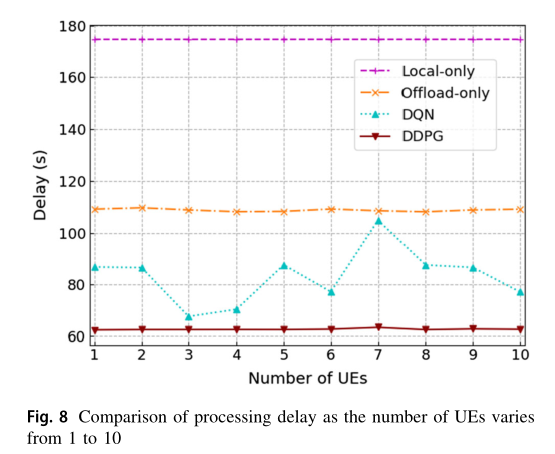
在图 8 中,我们比较了UE 的数量在1到10之间变化下 DDPG 方案、 DQN 、 Offload-only 和 Local-only 的平均处理延迟 。我们假设在不同数量的终端下,一个时间段内要完成的总任务大小是相同的。如图 8 所示,随着 UE 数量的增加,除 DQN 外,其他方案的平均处理延迟几乎不变。随着 UE 数量的增加, DQN 方案的处理延迟在 86 s左右波动。原因可以解释如下。不同数量 UE 的情况下, DQN 输出动作取值范围差异较大。因此,当样本作为 DQN 训练的输入时, DQN 可能倾向于输出更大的值。 DDPG 的演员网络输出多维动作,保证了 DNN 的输入数据在同一范围内,即 [0,1] ,保证了 DDPG 算法的收敛性和稳定性。此外,所提出的 DDPG 方案具有最小的延迟。这是因为 DDPG 方案能够在连续动作中找到最优值,从而得到最优控制策略。
6 结论
本文研究了无人机辅助的移动通信系统中的计算卸载问题,该系统由飞行无人机为终端提供通信和计算服务。通过联合优化用户调度、任务卸载率、无人机飞行角度和飞行速度,以最小化整个时间段内最大处理延迟之和为目标。为了解决离散变量非凸优化问题,引入了 DDPG 训练算法来获得最优卸载策略。我们描述了 RL 相关的背景知识和 DDPG 训练过程。然后,提出状态归一化算法,使 DDPG 算法更容易收敛。通过仿真分析了 DDPG 算法的参数,比较了不同参数的影响,包括学习率、折扣因子和训练策略。仿真结果表明,与基线算法相比,我们提出的算法在处理延迟方面有更好的性能。在未来的工作中,我们将研究我们的算法与其他流行的RL算法的性能,如 ACER , ACKTR , PRO2 和 TRPO 。











