莫烦强化学习-Q Leaning

参考链接：

https://mofanpy.com/tutorials/machine-learning/reinforcement-learning/intro-q-learning/

第2章 Q-learning

强化学习中有名的算法，Q-learning。由第一章可知，Q-learning的分类是model-free，基于价值，单步更新，离线学习。

2.1 什么是Q-Learning

2.1.1 行为准则

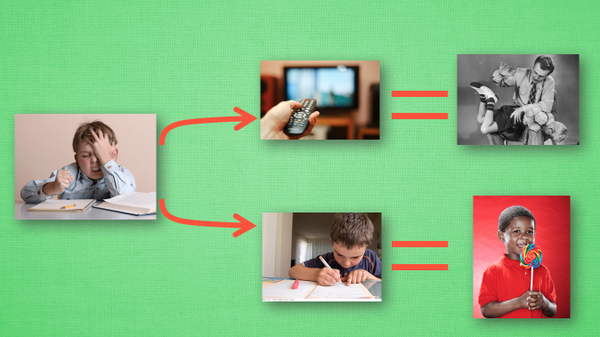
我们做事情都会有一个自己的行为准则, 比如小时候爸妈常说”不写完作业就不准看电视”。所以我们在 写作业的这种状态下, 好的行为就是继续写作业, 直到写完它, 我们还可以得到奖励, 不好的行为就是没写完就跑去看电视了, 被爸妈发现, 后果很严重。小时候这种事情做多了, 也就变成我们不可磨灭的记忆。这和我们要提到的 Q learning 有什么关系呢? 原来 Q learning 也是一个决策过程, 和小时候的这种情况差不多。我们举例说明.

假设现在我们处于写作业的状态而且我们以前并没有尝试过写作业时看电视, 所以现在我们有两种选择 , 1, 继续写作业, 2, 跑去看电视. 因为以前没有被罚过, 所以我选看电视, 然后现在的状态变成了看电视, 我又选了继续看电视, 接着我还是看电视, 最后爸妈回家, 发现我没写完作业就去看电视了, 狠狠地惩罚了我一次, 我也深刻地记下了这一次经历, 并在我的脑海中将 “没写完作业就看电视” 这种行为更改为负面行为, 我们在看看 Q learning 根据很多这样的经历是如何来决策的吧。

2.1.2 QLearning 决策

假设我们的行为准则已经学习好了, 现在我们处于状态s1, 我在写作业, 我有两个行为 a1, a2, 分别是看电视和写作业, 根据我的经验, 在这种 s1 状态下, a2 写作业带来的潜在奖励要比 a1 看电视高（比较不同决策的价值）, 这里的潜在奖励我们可以用一个有关于 s 和 a 的 Q 表格代替, 在我的记忆Q表格中, Q(s1, a1)=-2 要小于 Q(s1, a2)=1, 所以我们判断要选择 a2 作为下一个行为。现在我们的状态更新成 s2 , 我们还是有两个同样的选择, 重复上面的过程, 在行为准则Q 表中寻找 Q(s2, a1)和Q(s2, a2) 的值, 并比较他们的大小, 选取较大的一个。接着根据 a2 我们到达 s3 并在此重复上面的决策过程. Q learning 的方法也就是这样决策的。看完决策, 我看在来研究一下这张行为准则 Q 表是通过什么样的方式更改, 提升的。

2.1.3 QLearning 更新

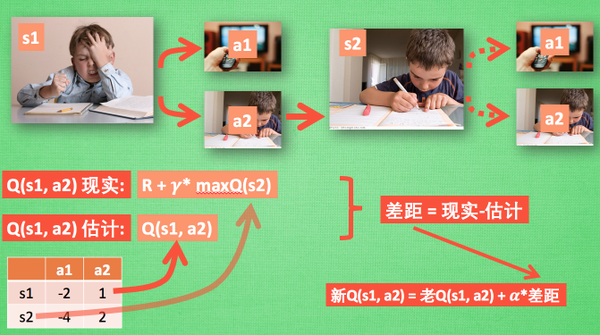
所以我们回到之前的流程, 根据 Q 表的估计, 因为在 s1 中, a2 的值比较大, 通过之前的决策方法, 我们在 s1 采取了 a2, 并到达 s2, 这时我们开始更新用于决策的 Q 表, 接着我们并没有在实际中采取任何行为, 而是再想象自己在 s2 上采取了每种行为, 分别看看两种行为哪一个的 Q 值大, 比如说 Q(s2, a2) 的值比 Q(s2, a1) 的大, 所以我们把大的 Q(s2, a2) 乘上一个衰减值 gamma (比如是0.9) 并加上到达s2时所获取的奖励 R (这里还没有获取到我们的棒棒糖, 所以奖励为 0), 因为会获取实实在在的奖励 R , 我们将这个作为我现实中 Q(s1, a2) 的值, 但是我们之前是根据 Q 表估计 Q(s1, a2) 的值。所以有了现实和估计值, 我们就能更新Q(s1, a2) , 根据估计与现实的差距, 将这个差距乘以一个学习效率 alpha 累加上老的 Q(s1, a2) 的值变成新的值。但时刻记住, 我们虽然用 maxQ(s2) 估算了一下 s2 状态, 但还没有在 s2 做出任何的行为, s2 的行为决策要等到更新完了以后再重新另外做。这就是 off-policy 的 Q learning 是如何决策和学习优化决策的过程。

2.1.4 QLearning 整体算法

这一张图概括了我们之前所有的内容。这也是 Q learning 的算法, 每次更新我们都用到了 Q 现实和 Q 估计, 而且 Q learning 的迷人之处就是 在 Q(s1, a2) 现实中, 也包含了一个 Q(s2) 的最大估计值, 将对下一步的衰减的最大估计和当前所得到的奖励当成这一步的现实, 很奇妙吧。最后我们来说说这套算法中一些参数的意义。Epsilon greedy 是用在决策上的一种策略, 比如 epsilon = 0.9 时, 就说明有90% 的情况我会按照 Q 表的最优值选择行为, 10% 的时间使用随机选行为。alpha是学习率, 来决定这次的误差有多少是要被学习的, alpha是一个小于1 的数。gamma 是对未来 reward 的衰减值。

2.1.5 QLearning 中的 Gamma

我们重写一下 Q(s1) 的公式, 将 Q(s2) 拆开, 因为Q(s2)可以像 Q(s1)一样,是关于Q(s3) 的, 所以可以写成这样, 然后以此类推, 不停地这样写下去, 最后就能写成这样。**可以看出Q(s1) 是有关于之后所有的奖励, 但这些奖励正在衰减, 离 s1 越远的状态衰减越严重。**不好理解? 行, 我们想象 Qlearning 的机器人天生近视眼, gamma = 1 时, 机器人有了一副合适的眼镜, 在 s1 看到的 Q 是未来没有任何衰变的奖励, 也就是机器人能清清楚楚地看到之后所有步的全部价值, 但是当 gamma =0, 近视机器人没了眼镜, 只能摸到眼前的 reward, 同样也就只在乎最近的大奖励, 如果 gamma 从 0 变到 1, 眼镜的度数由浅变深, 对远处的价值看得越清楚, 所以机器人渐渐变得有远见, 不仅仅只看眼前的利益, 也为自己的未来着想。

2.1.6 补充

1.为什么不直接用现实值更新老的Q值呢？

Q值是未来发展情况的累计变量，不只有下一步的现实值

Q值的定义，从当前状态开始，之后每一次状态决策都采取最优解，直到最后一个状态（Game over）的动作质量(quality)。

Q值可以一眼看穿未来，这就是Q-learning 的迷人之处。

奖励表 R 是自然生成客观存在的。

2.2 小例子

2.2.1 要点

这一次我们会用 tabular Q-learning 的方法实现一个小例子, 例子的环境是一个一维世界, 在世界的右边有宝藏, 探索者只要得到宝藏尝到了甜头, 然后以后就记住了得到宝藏的方法, 这就是他用强化学习所学习到的行为。

-o---T
# T 就是宝藏的位置, o 是探索者的位置

Q-learning 是一种记录行为值 (Q value) 的方法, 每种在一定状态的行为都会有一个值 Q(s, a), 就是说行为 a 在 s 状态的值是 Q(s, a)。 s 在上面的探索者游戏中, 就是 o 所在的地点了。 而每一个地点探索者都能做出两个行为 left/right, 这就是探索者的所有可行的 a 啦。

如果在某个地点 s1, 探索者计算了他能有的两个行为, a1/a2=left/right, 计算结果是 Q(s1, a1) > Q(s1, a2), 那么探索者就会选择 left 这个行为。 这就是 Q learning 的行为选择简单规则。

当然我们还会细说更具体的规则。 在之后的教程中, 我们会更加详细得讲解 RL 中的各种方法, 下面的内容, 大家大概看看就行, 有个大概的 RL 概念就行, 知道 RL 的一些关键步骤就行, 这节的算法不用仔细研究。

2.2.2 预设值

这一次需要的模块和参数设置:

import numpy as np
import pandas as pd
import time

N_STATES = 6   # 1维世界的宽度
ACTIONS = ['left', 'right']     # 探索者的可用动作
EPSILON = 0.9   # 贪婪度 greedy
ALPHA = 0.1     # 学习率
GAMMA = 0.9    # 奖励递减值
MAX_EPISODES = 13   # 最大回合数
FRESH_TIME = 0.3    # 移动间隔时间

2.2.3 Q 表

对于 tabular Q learning, 我们必须将所有的 Q values (行为值) 放在 q_table 中, 更新 q_table 也是在更新他的行为准则。 q_table 的 index 是所有对应的 state (探索者位置), columns 是对应的 action (探索者行为)。

def build_q_table(n_states, actions):
    table = pd.DataFrame(
        np.zeros((n_states, len(actions))),     # q_table 全 0 初始
        columns=actions,    # columns 对应的是行为名称
    )
    return table

# q_table:
"""
   left  right
0   0.0    0.0
1   0.0    0.0
2   0.0    0.0
3   0.0    0.0
4   0.0    0.0
5   0.0    0.0
"""

2.2.4 定义动作

接着定义探索者是如何挑选行为的。 这是我们引入 epsilon greedy 的概念。 因为在初始阶段, 随机的探索环境, 往往比固定的行为模式要好, 所以这也是累积经验的阶段, 我们希望探索者不会那么贪婪(greedy)。 所以 EPSILON 就是用来控制贪婪程度的值。 EPSILON 可以随着探索时间不断提升(越来越贪婪), 不过在这个例子中, 我们就固定成 EPSILON = 0.9, 90% 的时间是选择最优策略, 10% 的时间来探索。

# 在某个 state 地点, 选择行为
def choose_action(state, q_table):
    state_actions = q_table.iloc[state, :]  # 选出这个 state 的所有 action 值
    if (np.random.uniform() > EPSILON) or (state_actions.all() == 0):  # 非贪婪 or 或者这个 state 还没有探索过
        action_name = np.random.choice(ACTIONS)
    else:
        action_name = state_actions.argmax()    # 贪婪模式
    return action_name

2.2.5 环境反馈 S_, R

做出行为后, 环境也要给我们的行为一个反馈, 反馈出下个 state (S_) 和 在上个 state (S) 做出 action (A) 所得到的 reward ®。 这里定义的规则就是, 只有当 o 移动到了 T, 探索者才会得到唯一的一个奖励, 奖励值 R=1, 其他情况都没有奖励。

def get_env_feedback(S, A):
    # This is how agent will interact with the environment
    if A == 'right':    # move right
        if S == N_STATES - 2:   # terminate
            S_ = 'terminal'
            R = 1
        else:
            S_ = S + 1
            R = 0
    else:   # move left
        R = 0
        if S == 0:
            S_ = S  # reach the wall
        else:
            S_ = S - 1
    return S_, R

2.2.6 环境更新

接下来就是环境的更新了, 不用细看。

def update_env(S, episode, step_counter):
    # This is how environment be updated
    env_list = ['-']*(N_STATES-1) + ['T']   # '---------T' our environment
    if S == 'terminal':
        interaction = 'Episode %s: total_steps = %s' % (episode+1, step_counter)
        print('\r{}'.format(interaction), end='')
        time.sleep(2)
        print('\r                                ', end='')
    else:
        env_list[S] = 'o'
        interaction = ''.join(env_list)
        print('\r{}'.format(interaction), end='')
        time.sleep(FRESH_TIME)

2.2.7 强化学习主循环

最重要的地方就在这里。 你定义的 RL 方法都在这里体现。 在之后的教程中, 我们会更加详细得讲解 RL 中的各种方法, 下面的内容, 大家大概看看就行, 这节内容不用仔细研究。

def rl():
    q_table = build_q_table(N_STATES, ACTIONS)  # 初始 q table
    for episode in range(MAX_EPISODES):     # 回合
        step_counter = 0
        S = 0   # 回合初始位置
        is_terminated = False   # 是否回合结束
        update_env(S, episode, step_counter)    # 环境更新
        
        while not is_terminated:
            A = choose_action(S, q_table)   # 选行为
            S_, R = get_env_feedback(S, A)  # 实施行为并得到环境的反馈
            q_predict = q_table.loc[S, A]    # 估算的(状态-行为)值
            if S_ != 'terminal':
                q_target = R + GAMMA * q_table.iloc[S_, :].max()   #  实际的(状态-行为)值 (回合没结束)
            else:
                q_target = R     #  实际的(状态-行为)值 (回合结束)
                is_terminated = True    # terminate this episode

            q_table.loc[S, A] += ALPHA * (q_target - q_predict)  #  q_table 更新
            S = S_  # 探索者移动到下一个 state

            update_env(S, episode, step_counter+1)  # 环境更新

            step_counter += 1
    return q_table

写好所有的评估和更新准则后, 我们就能开始训练了, 把探索者丢到环境中, 让它自己去玩吧。

if __name__ == "__main__":
    q_table = rl()
    print('\r\nQ-table:\n')
    print(q_table)

2.2.8 补充

1.运行到q_predict = q_table.loc[S, A]出现了一个KeyError。

解决方式：把action_name = state_actions.argmax()改成action_name = ACTIONS[state_actions.argmax()]就可以了。

2.3 Q-learning 算法更新

2.3.1 要点

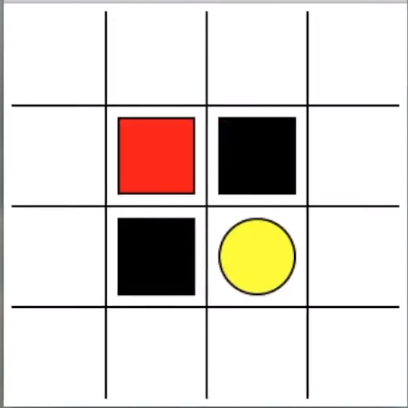
上次我们知道了 RL 之中的 Q-learning 方法是在做什么事, 今天我们就来说说一个更具体的例子。让探索者学会走迷宫。黄色的是天堂 (reward 1), 黑色的地狱 (reward -1)。大多数 RL 是由 reward 导向的, 所以定义 reward 是 RL 中比较重要的一点。

2.3.2 算法

**整个算法就是一直不断更新 Q table 里的值, 然后再根据新的值来判断要在某个 state 采取怎样的 action。**Qlearning 是一个 off-policy 的算法, 因为里面的 max action 让 Q table 的更新可以不基于正在经历的经验(可以是现在学习着很久以前的经验,甚至是学习他人的经验)。不过这一次的例子, 我们没有运用到 off-policy, 而是把 Qlearning 用在了 on-policy 上, 也就是现学现卖, 将现在经历的直接当场学习并运用。

2.3.3 算法的代码形式

首先我们先 import 两个模块, maze_env 是我们的环境模块, 已经编写好了, 大家可以直接在这里下载, maze_env 模块我们可以不深入研究, 如果你对编辑环境感兴趣, 可以去看看如何使用 python 自带的简单 GUI 模块 tkinter 来编写虚拟环境. 我也有对应的教程。maze_env 就是用 tkinter 编写的. 而 RL_brain 这个模块是 RL 的大脑部分, 我们下节会讲。

from maze_env import Maze
from RL_brain import QLearningTable

下面的代码, 我们可以根据上面的图片中的算法对应起来, 这就是整个 Qlearning 最重要的迭代更新部分啦。

def update():
    # 学习 100 回合
    for episode in range(100):
        # 初始化 state 的观测值
        observation = env.reset()

        while True:
            # 更新可视化环境
            env.render()

            # RL 大脑根据 state 的观测值挑选 action
            action = RL.choose_action(str(observation))

            # 探索者在环境中实施这个 action, 并得到环境返回的下一个 state 观测值, reward 和 done (是否是掉下地狱或者升上天堂)
            observation_, reward, done = env.step(action)

            # RL 从这个序列 (state, action, reward, state_) 中学习
            RL.learn(str(observation), action, reward, str(observation_))

            # 将下一个 state 的值传到下一次循环
            observation = observation_

            # 如果掉下地狱或者升上天堂, 这回合就结束了
            if done:
                break

    # 结束游戏并关闭窗口
    print('game over')
    env.destroy()

if __name__ == "__main__":
    # 定义环境 env 和 RL 方式
    env = Maze()
    RL = QLearningTable(actions=list(range(env.n_actions)))

    # 开始可视化环境 env
    env.after(100, update)
    env.mainloop()

2.3.4 补充

1.为什么训练的时候，红色方框会斜着走？

应该是 tkinter 的跳帧问题，实际上还是走了 2 步

2.observation的初始值（5，5，35，35）对应成我们可以理解的坐标（x,y），这应该是怎么转换的呢？

是正方形的x1,y1,x2,y2 坐标。

3.您好，我看maze_env的代码时，没有看到针对不同state对action的限制。
比如当已经走到maze的边界，这时不需要限制方块的行为吗？运行run this后，发现方块在边界的移动刷新速率并不总相同，是否因为上述action未受限？

在maze_env.py的第95行有限制。

if action == 0:
    if s[1] > UNIT:
        base_action[1] -= UNIT
elif action == 1:   
    if s[1] < (MAZE_H - 1) * UNIT:
        base_action[1] += UNIT
elif action == 2:   
    if s[0] < (MAZE_W - 1) * UNIT:
        base_action[0] += UNIT
elif action == 3:   
    if s[0] > UNIT:
        base_action[0] -= UNIT

但是在rl的action输出上，不会对上下左右动作做限制。

2.4 Q-learning 思维决策

2.4.1 代码主结构

与上回不一样的地方是, 我们将要以一个 class 形式定义 Q learning, 并把这种 tabular q learning 方法叫做 QLearningTable。

class QLearningTable:
    # 初始化
    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):

    # 选行为
    def choose_action(self, observation):

    # 学习更新参数
    def learn(self, s, a, r, s_):

    # 检测 state 是否存在
    def check_state_exist(self, state):

2.4.2 预设值

import numpy as np
import pandas as pd


class QLearningTable:
    def __init__(self, actions, learning_rate=0.01, reward_decay=0.9, e_greedy=0.9):
        self.actions = actions  # a list
        self.lr = learning_rate # 学习率
        self.gamma = reward_decay   # 奖励衰减
        self.epsilon = e_greedy     # 贪婪度
        self.q_table = pd.DataFrame(columns=self.actions, dtype=np.float64)   # 初始 q_table

2.4.3 决定行为

这里是定义如何根据所在的 state, 或者是在这个 state 上的 观测值 (observation) 来决策。

def choose_action(self, observation):
        self.check_state_exist(observation) # 检测本 state 是否在 q_table 中存在(见后面标题内容)

        # 选择 action
        if np.random.uniform() < self.epsilon:  # 选择 Q value 最高的 action
            state_action = self.q_table.loc[observation, :]

            # 同一个 state, 可能会有多个相同的 Q action value, 所以我们乱序一下
            action = np.random.choice(state_action[state_action == np.max(state_action)].index)

        else:   # 随机选择 action
            action = np.random.choice(self.actions)

        return action

2.4.4 学习

同上一个简单的 q learning 例子一样, 我们根据是否是 terminal state (回合终止符) 来判断应该如何更行 q_table. 更新的方式是不是很熟悉呢:

update = self.lr * (q_target - q_predict)

这可以理解成神经网络中的更新方式, 学习率 * (真实值 - 预测值). 将判断误差传递回去, 有着和神经网络更新的异曲同工之处。

def learn(self, s, a, r, s_):
        self.check_state_exist(s_)  # 检测 q_table 中是否存在 s_ (见后面标题内容)
        q_predict = self.q_table.loc[s, a]
        if s_ != 'terminal':
            q_target = r + self.gamma * self.q_table.loc[s_, :].max()  # 下个 state 不是 终止符
        else:
            q_target = r  # 下个 state 是终止符
        self.q_table.loc[s, a] += self.lr * (q_target - q_predict)  # 更新对应的 state-action 值

2.4.5 检测 state 是否存在

这个功能就是检测 q_table 中有没有当前 state 的步骤了, 如果还没有当前 state, 那我们就插入一组全 0 数据, 当做这个 state 的所有 action 初始 values。

def check_state_exist(self, state):
        if state not in self.q_table.index:
            # append new state to q table
            self.q_table = self.q_table.append(
                pd.Series(
                    [0]*len(self.actions),
                    index=self.q_table.columns,
                    name=state,
                )
            )