1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
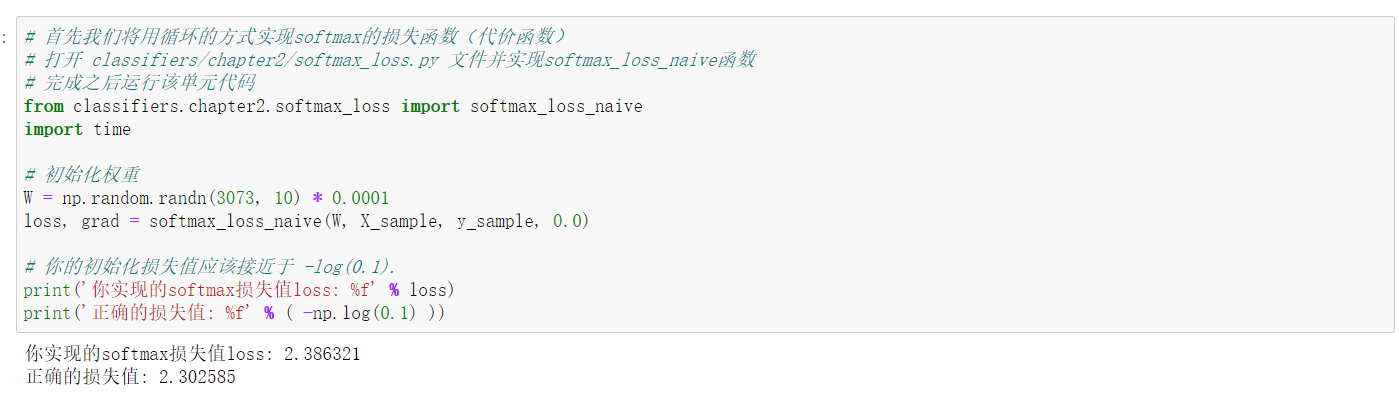
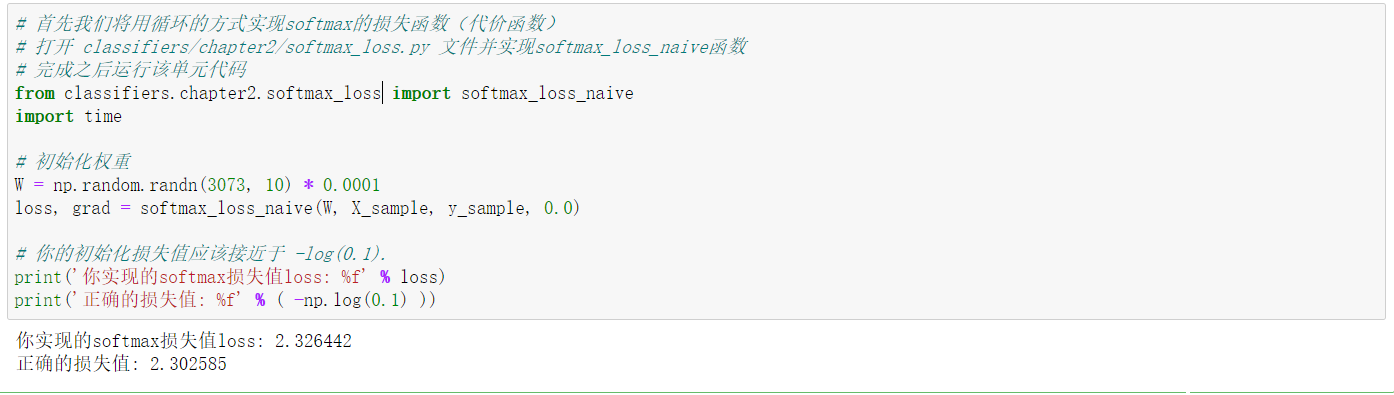
| def softmax_loss_naive(W, X, y, reg):
"""
使用显式循环版本计算Softmax损失函数
N表示:数据个数,D表示:数据维度,C:表示数据类别个数。
Inputs:
- W: 形状(D, C) numpy数组,表示分类器权重(参数).
- X: 形状(N, D) numpy数组,表示训练数据.
- y: 形状(N,) numpy数组,表示数据类标。
其中 y[i] = c 意味着X[i]为第c类数据,c取值为[0,c)
- reg: 正则化惩罚系数
Returns 二元组(tuple):
- loss,数据损失值
- dW,权重W所对应的梯度,其形状和W相同
"""
loss = 0.0
dW = np.zeros_like(W)
N = X.shape[0]
C = W.shape[1]
result = X.dot(W)
result -= np.max(result,axis=1,keepdims=True)
for i in range(N):
soft_max = np.exp(result[i][y[i]])/np.sum(np.exp(result[i]))
loss += -np.log(soft_max)
for j in range(C):
if j==y[i]:
dW[:,j] += -X[i].T
dW[:,j] += (X[i].T * np.exp(result[i][j])) / (np.sum(np.exp(result[i])))
loss/= N
loss += reg*np.sum(W*W)
dW /= N
dW += reg*2*W
return loss, dW
|