R做多元线性回归全攻略

参考链接：

https://www.jianshu.com/p/4c6c8174f292

R中的线性回归函数比较简单，就是lm()，比较复杂的是对线性模型的诊断和调整。这里结合Statistical Learning和杜克大学的Data Analysis and Statistical Inference的章节以及《R语言实战》的OLS(Ordinary Least Square)回归模型章节来总结一下，诊断多元线性回归模型的操作分析步骤。

1、选择预测变量

因变量比较容易确定，多元回归模型中难在自变量的选择。自变量选择主要可分为向前选择（逐次加使RSS最小的自变量），向后选择（逐次扔掉p值最大的变量）。个人倾向于向后选择法，一来p值比较直观，模型返回结果直接给出了各变量的p值，却没有直接给出RSS；二来当自变量比较多时，一个个加比较麻烦。

Call:
lm(formula = Sales ~ . + Income:Advertising + Age:Price, data = Carseats)
Residuals:
Min      1Q  Median      3Q     Max
-2.9208 -0.7503  0.0177  0.6754  3.3413
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)         6.5755654  1.0087470   6.519 2.22e-10 ***
CompPrice           0.0929371  0.0041183  22.567  < 2e-16 ***
Income              0.0108940  0.0026044   4.183 3.57e-05 ***
Advertising         0.0702462  0.0226091   3.107 0.002030 **
Population          0.0001592  0.0003679   0.433 0.665330
Price              -0.1008064  0.0074399 -13.549  < 2e-16 ***
ShelveLocGood       4.8486762  0.1528378  31.724  < 2e-16 ***
ShelveLocMedium     1.9532620  0.1257682  15.531  < 2e-16 ***
Age                -0.0579466  0.0159506  -3.633 0.000318 ***
Education          -0.0208525  0.0196131  -1.063 0.288361
UrbanYes            0.1401597  0.1124019   1.247 0.213171
USYes              -0.1575571  0.1489234  -1.058 0.290729
Income:Advertising  0.0007510  0.0002784   2.698 0.007290 **
Price:Age           0.0001068  0.0001333   0.801 0.423812
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.011 on 386 degrees of freedom
Multiple R-squared:  0.8761,    Adjusted R-squared:  0.8719
F-statistic:   210 on 13 and 386 DF,  p-value: < 2.2e-16

构建一个回归模型后，先看F统计量的p值，这是对整个模型的假设检验，原假设是各系数都为0，如果连这个p值都不显著，无法证明至少有一个自变量对因变量有显著性影响，这个模型便不成立。然后看Adjusted R2，每调整一次模型，应该使它变大；Adjusted R2越大说明模型中相关的自变量对因变量可解释的变异比例越大，模型的预测性就越好。

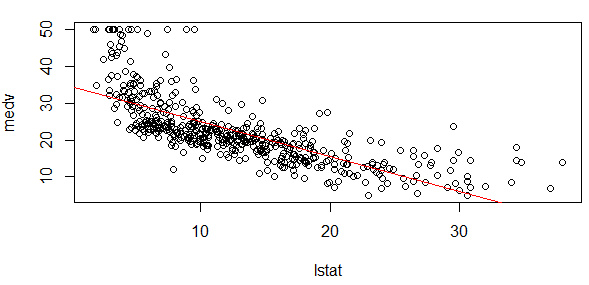
构建了线性模型后，如果是一元线性回归，可以画模型图初步判断一下线性关系（多元回归模型不好可视化）：

par(mfrow=c(1,1))
plot(medv~lstat,Boston)
fit1=lm(medv~lstat,data=Boston)
abline(fit1,col="red")

2、模型诊断

确定了回归模型的自变量并初步得到一个线性回归模型，并不是直接可以拿来用的，还要进行验证和诊断。诊断之前，先回顾多元线性回归模型的假设前提（by Data Analysis and Statistical Inference）：

（数值型）自变量要与因变量有线性关系；

残差基本呈正态分布；

残差方差基本不变（同方差性）；

残差（样本）间相关独立。

一个好的多元线性回归模型应当尽量满足这4点假设前提。

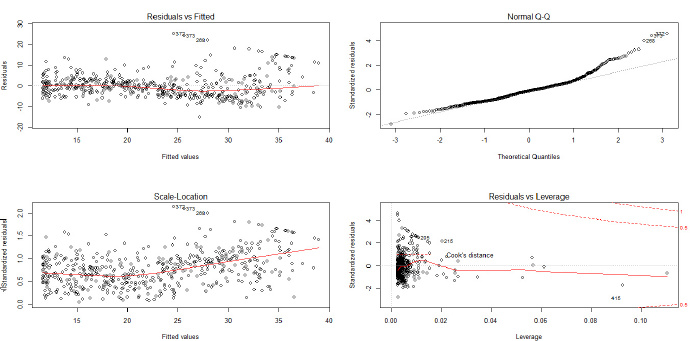
用lm()构造一个线性模型fit后，plot(fit)即可返回4张图（可以par(mfrow=c(2,2))一次展现），这4张图可作初步检验：

左上图用来检验假设1，如果散点看不出什么规律，则表示线性关系良好，若有明显关系，则说明非线性关系明显。右上图用来检验假设2，若散点大致都集中在QQ图中的直线上，则说明残差正态性良好。左下图用来检验假设3，若点在曲线周围随机分布，则可认为假设3成立；若散点呈明显规律，比如方差随均值而增大，则越往右的散点上下间距会越大，方差差异就越明显。假设4的独立性无法通过这几张图来检验，只能通过数据本身的来源的意义去判断。

右下图是用来检验异常值。异常值与三个概念有关：

离群点：y远离散点主体区域的点

杠杆点：x远离散点主体区域的点，一般不影响回归直线的斜率

强影响点：影响回归直线的斜率，一般是高杠杆点。

对于多元线性回归，高杠杆点不一定就是极端点，有可能是各个变量的取值都正常，但仍然偏离散点主体。

对于异常值，可以谨慎地删除，看新的模型是否效果更好。

《R语言实战》里推荐了更好的诊断方法，总结如下。

1、多元线性回归假设验证：

gvlma包的gvlma()函数可对拟合模型的假设作综合验证，并对峰度、偏度进行验证。

states <- as.data.frame(state.x77[, c("Murder", "Population",
"Illiteracy", "Income", "Frost")])
fit <- lm(Murder ~ Population + Illiteracy + Income +
Frost, data = states)
library(gvlma)
gvmodel <- gvlma(fit)
summary(gvmodel)
Call:
gvlma(x = fit)
Value p-value                Decision
Global Stat        2.7728  0.5965 Assumptions acceptable.
Skewness           1.5374  0.2150 Assumptions acceptable.
Kurtosis           0.6376  0.4246 Assumptions acceptable.
Link Function      0.1154  0.7341 Assumptions acceptable.
Heteroscedasticity 0.4824  0.4873 Assumptions acceptable.

最后的Global Stat是对4个假设条件进行综合验证，通过了即表示4个假设验证都通过了。最后的Heterosceasticity是进行异方差检测。注意这里假设检验的原假设都是假设成立，所以当p>0.05时，假设才能能过验证。

如果综合验证不通过，也有其他方法对4个假设条件分别验证：

线性假设

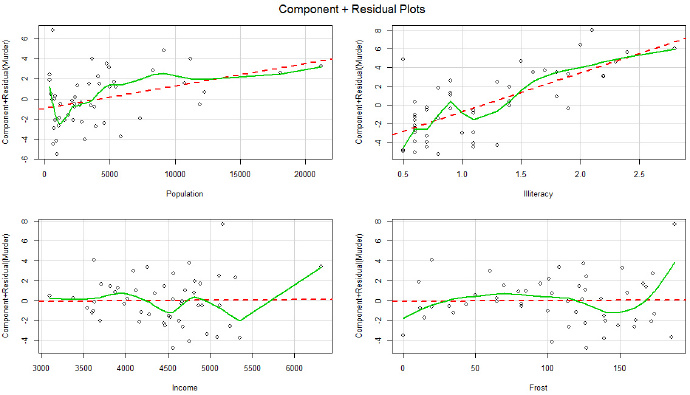
library(car)
crPlots(fit)

返回的图是各个自变量与残差（因变量）的线性关系图，若存着明显的非线性关系，则需要对自变量作非线性转化。书中说这张图表明线性关系良好。

正态性

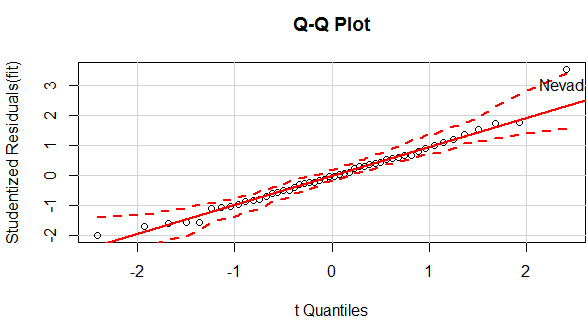
library(car)
qqPlot(fit,labels = row.names(states),id.method = "identify",simulate = TRUE,main = "Q-Q Plot")

qqPlot()可以生成交互式的qq图，选中异常点，就返回该点的名称。该图中除了Nevad点，其他点都在直线附近，可见正态性良好。

同方差性

library(car)
ncvTest(fit)
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 1.746514    Df = 1     p = 0.1863156

p值大于0.05，可认为满足方差相同的假设。

独立性

library(car)
durbinWatsonTest(fit)
lag Autocorrelation D-W Statistic p-value
1      -0.2006929      2.317691   0.258
Alternative hypothesis: rho != 0

p值大于0.05，可认为误差之间相互独立。

除了以上4点基本假设，还有其他方面需要进行诊断——

2、多重共线性

理想中的线性模型各个自变量应该是线性无关的，若自变量间存在共线性，则会降低回归系数的准确性。一般用方差膨胀因子VIF(Variance Inflation Factor)来衡量共线性，《统计学习》中认为VIF超过5或10就存在共线性，《R语言实战》中认为VIF大于4则存在共线性。理想中的线性模型VIF=1，表完全不存在共线性。

library(car)
vif(fit)
Population Illiteracy     Income      Frost
1.245282   2.165848   1.345822   2.082547

可见这4个自变量VIF都比较小，可认为不存在多重共线性的问题。

3、异常值检验

离群点

离群点有三种判断方法：一是用qqPlot()画QQ图，落在置信区间（上图中两条虚线）外的即可认为是离群点，如上图中的Nevad点；一种是判断学生标准化残差值，绝对值大于2（《R语言实战》中认为2，《统计学习》中认为3）的可认为是离群点。

plot(x=fitted(fit),y=rstudent(fit))
abline(h=3,col="red",lty=2)
abline(h=-3,col="red",lty=2)
which(abs(rstudent(fit))>3)
Nevada
28

还有一种方法是利用car包里的outlierTest()函数进行假设检验：

library(car)
outlierTest(fit)
rstudent unadjusted p-value Bonferonni p
Nevada 3.542929         0.00095088     0.047544

这个函数用来检验最大的标准化残差值，如果p>0.05，可以认为没有离群点；若p<0.05，则该点是离群点，但不能说明只有一个离群点，可以把这个点删除之后再作检验。第三种方法可以与第二种方法结合起来使用。

高杠杆点

高杠杆值观测点，即是与其他预测变量有关的离群点。换句话说，它们是由许多异常的预测变量值组合起来的，与响应变量值没有关系。《统计学习》中给出了一个杠杆统计量，《R语言实战》中给出了一种具体的操作方法。（两本书也稍有出入，《统计学习》中平均杠杆值为(p+1)/n，而在《R语言实战》中平均杠杆值为p/n；事实上在样本量n比较大时，几乎没有差别。）

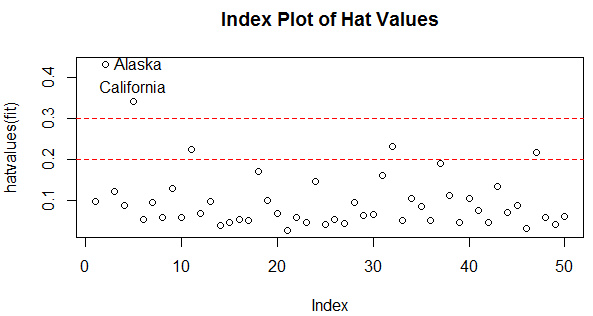
hat.plot <- function(fit){
p <- length(coefficients(fit))
n <- length(fitted(fit))
plot(hatvalues(fit),main = "Index Plot of Hat Values")
abline(h=c(2,3)*p/n,col="red",lty=2)
identify(1:n, hatvalues(fit), names(hatvalues(fit)))  #这句产生交互效果，选中某个点后，关闭后返回点的名称
}
hat.plot(fit)

超过2倍或3倍的平均杠杆值即可认为是高杠杆点，这里把Alaska和California作为高杠杆点。

强影响点

强影响点是那种若删除则模型的系数会产生明显的变化的点。一种方法是计算Cook距离，一般来说， Cook’s D值大于4/(n-k -1)，则表明它是强影响点，其中n 为样本量大小， k 是预测变量数目。

cutoff <- 4/(nrow(states-length(fit$coefficients)-2)) #coefficients加上了截距项，因此要多减1
plot(fit,which=4,cook.levels = cutoff)
abline(h=cutoff,lty=2,col="red")

作者：真依然很拉风
链接：https://www.jianshu.com/p/4c6c8174f292
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。