【数据挖掘】使用R语言进行聚类分析

本文主要介绍在R语言中使用k-means和K-Medoids进行聚类分析的方法。

一、首先介绍下聚类分析中主要的算法：

K-均值聚类（K-Means） 十大经典算法

K-中心点聚类（K-Medoids）

密度聚类（DBSCAN）

系谱聚类（HC）

期望最大化聚类（EM） 十大经典算法

聚类算法软件包主要函数
K-meansstatskmeans()
K-Medoidsclusterpam()
系谱聚类（HC）statshclust(), cutree(), rect.hclust()
密度聚类（DBSCAN）fpcdbscan()
期望最大化聚类（EM）mclustMclust(), clustBIC(), mclust2Dplot(), densityMclust()

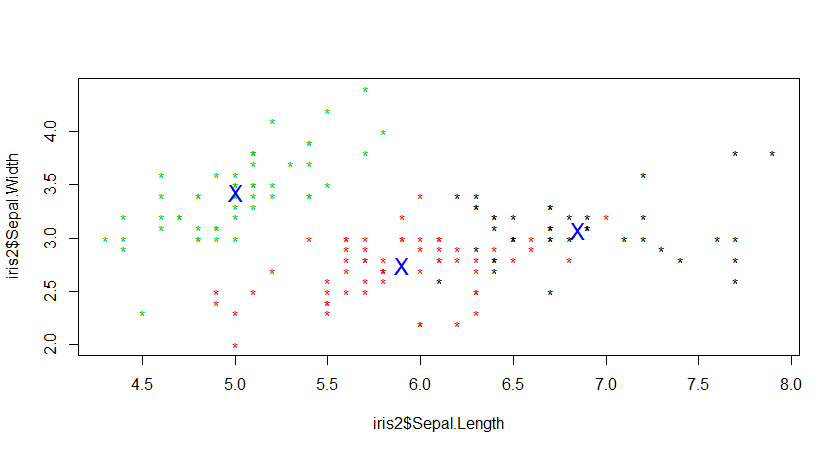
二、用iris数据集进行kmeans分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# kmeans对iris进行聚类分析 
 
iris2<-iris[,1:4]
iris.kmeans<-kmeans(iris2,3)
iris.kmeans
 
#用table函数查看分类结果情况
table(iris$Species,iris.kmeans$cluster)
 
# 1  2  3
# setosa     50  0  0
# versicolor  0 48  2
# virginica   0 14 36
 
# K-means clustering with 3 clusters of sizes 50, 62, 38
 
# Cluster means:
#   Sepal.Length Sepal.Width Petal.Length Petal.Width
# 1     5.006000    3.428000     1.462000    0.246000
# 2     5.901613    2.748387     4.393548    1.433871
# 3     6.850000    3.073684     5.742105    2.071053
# 
# Clustering vector:
#   [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 3 2 2
# [56] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 3 3 3 3 2 3 3 3
# [111] 3 3 3 2 2 3 3 3 3 2 3 2 3 2 3 3 2 2 3 3 3 3 3 2 3 3 3 3 2 3 3 3 2 3 3 3 2 3 3 2
# 
# Within cluster sum of squares by cluster:
#   [1] 15.15100 39.82097 23.87947
# (between_SS / total_SS =  88.4 %)
# 
# Available components:
#   
#   [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss" "betweenss"    "size"        
# [8] "iter"         "ifault" 
#在上述属性中，最常用的就是centers和cluster属性，即中心点和聚类的分类集合
 
#下边我们将分类以及中心点打印出来
 
plot(iris2$Sepal.Length,iris2$Sepal.Width,col=iris.kmeans$cluster,pch="*")
 
points(iris.kmeans$centers,pch="X",cex=1.5,col=4)

1

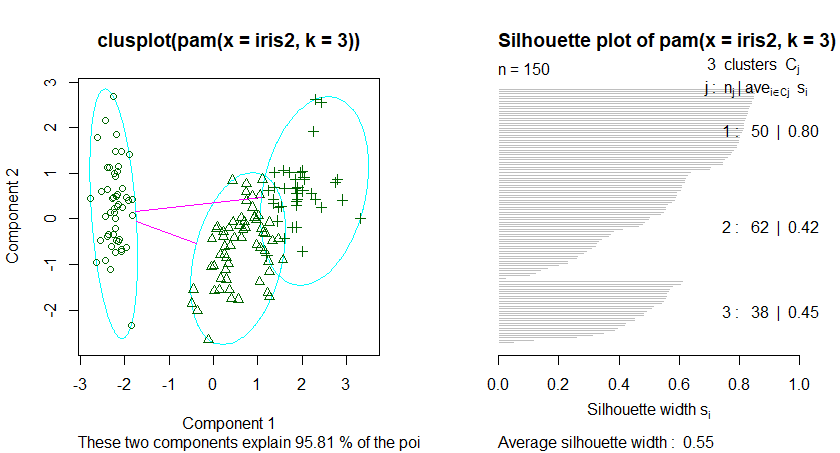
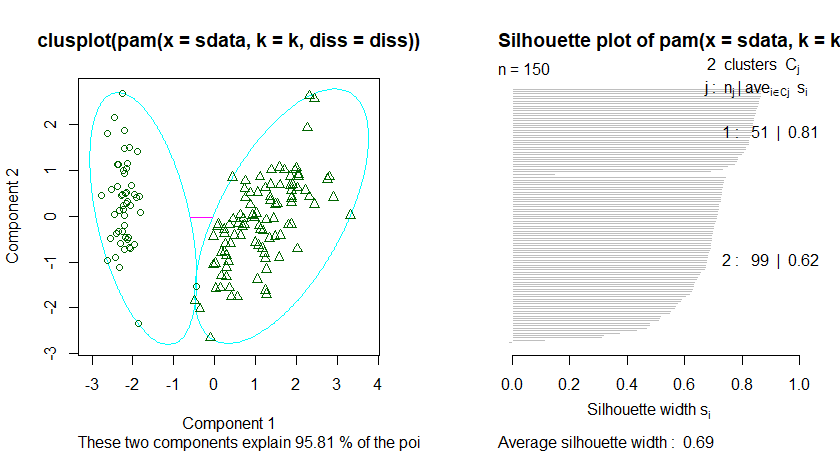
三、使用K-Mediods 进行聚类分析

K-Mediods函数跟Kmeans函数基本类似，不同的是，Kmeans是选择簇中心来表示聚类簇，而K-Mediods选择靠近簇中心的对象来表示聚类簇。在含有离群点的情况，下K-Mediods的鲁棒性（稳定性）要更好。

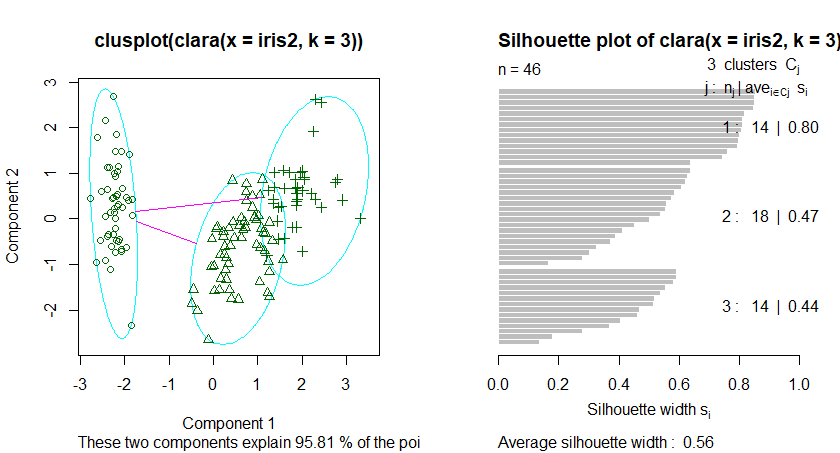
基于中心点的划分算法PAM是K-Mediods中的经典算法，但是PAM很难扩展到较大数据集上，而Clara算法是对PAM算法的改进，他是在较大数据集中分为几个小数据集，分别进行PAM算法，并返回最好的聚类。因此在处理较大数据集的情况下CLARA算法要优于PAM算法，

在R的cluster包中的PAM和CLARA函数分别实现了上述两个算法，但是这两个函数都需要用户指定k值，即中心点的个数。fpc包中的pamk()函数提供了更加强大的算法，该函数不要求用户输入k值，而是自动调用pam或者clara来根据最优平均阴影宽度来估计聚类簇个数来划分数据集。

K-mediods算法描述

a) 首先随机选取一组聚类样本作为中心点集

b) 每个中心点对应一个簇

c) 计算各样本点到各个中心点的距离（如欧几里德距离），将样本点放入距离中心点最短的那个簇中

d) 计算各簇中，距簇内各样本点距离的绝度误差最小的点，作为新的中心点

e) 如果新的中心点集与原中心点集相同，算法终止；如果新的中心点集与原中心点集不完全相同，返回b)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#-----使用K-mediods方法来进行聚类分析
#k-mediods中包含pam、clara、pamk三种算法，我们通过iris数据集来看看三者表现
 
install.packages("cluster")
library(cluster)
 
iris2.pam<-pam(iris2,3)
table(iris$Species,iris2.pam$clustering)
 
#             1  2  3
# setosa     50  0  0
# versicolor  0 48  2
# virginica   0 14 36
 
layout(matrix(c(1,2),1,2)) #每页显示两个图
plot(iris2.pam)
layout(matrix(1))

2

1
2
3
4
5
6
7
8
9
10
11
iris2.clara<-clara(iris2,3)
table(iris$Species,iris2.clara$clustering)
 
#             1  2  3
# setosa     50  0  0
# versicolor  0 48  2
# virginica   0 13 37
 
layout(matrix(c(1,2),1,2)) #每页显示两个图
plot(iris2.clara)
layout(matrix(1))

3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
install.packages("fpc")
library(fpc)
iris2.pamk<-pamk(iris2)
table(iris2.pamk$pamobject$clustering,iris$Species)
 
 
layout(matrix(c(1,2),1,2)) #每页显示两个图
plot(iris2.pamk$pamobject)
layout(matrix(1))
 
#     setosa versicolor virginica
# 1     50          1         0
# 2      0         49        50
 
#通过上述分类结果可以看到，pam和calra算法分类结果基本类似，但是pamk将三类分为了两类。。

4

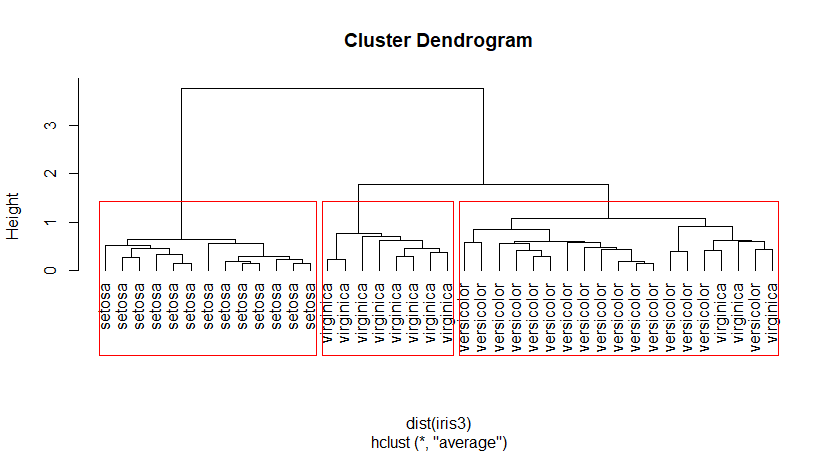
四、层次聚类HCluster

基本思想：

1、开始时，将每个样本作为一类。

2、规定某种度量作为样本之间距离以及类距离之间的度量，并且计算之。（hculster里边的dist方法以及method属性）

3、将距离最短的两个类合并为一个类。

4、重复2-3，即不断合并最近的两个类，每次减少一个类，直到所有的样本合并为一个类。

点与点的距离和类与类之间距离的计算可以参考R-modeling关于距离的介绍。

1
2
3
4
5
6
7
8
9
10
11
12
#---层次聚类 
dim(iris)#返回行列数
 
idx<-sample(1:dim(iris)[1],40)
iris3<-iris[idx,-5]
iris3
hc<-hclust(dist(iris3),method = "ave")  #注意hcluster里边传入的是dist返回值对象
 
plot(hc,hang=-1,labels=iris$Species[idx])  #这里的hang=-1使得树的节点在下方对齐
#将树分为3块
rect.hclust(hc,k=3)  
groups<-cutree(hc,k=3)

5

五、基于密度的聚类

前边的k-Means和k-Mediods算法比较适用于簇为球型的，对于非球型的，一般需要基于密度的聚类，比如DBSCAN

要了解DBSCAN，我们需要知道几个基本概念

  • r-邻域：给定点半径为r的区域。

  • 核心点：如果一个点的r邻域内最少包含M个点，则该点称为核心点。

  • 直接密度可达：对于核心点P而言，如果另一个点O在P的r邻域内，那么称O为P的直接密度可达点。

  • 密度可达：对于P的直接密度可达点O的r邻域内，如果包含另一个点Q，那么称Q为P的密度可达点。

  • 密度相连：如果Q和N都是核心点P的密度可达点，但是并不在一条直线路径上，那么称两者为密度相连。

算法思想：

  1. 指定R和M。
  2. 计算所有的样本点，如果点p的r邻域内有超过M个点，那么创建一个以P为核心点的新簇。
  3. 反复寻找这些核心点的直接密度可达点（之后可能是密度可达），将其加入到相应的簇，对于核心点发生密度相连的情况加以合并。
  4. 当没有新的点加入到任何簇中时，算法结束。

优点：

（1）聚类速度快且能够有效处理噪声点和发现任意形状的空间聚类；

（2）与K-MEANS比较起来，不需要输入要划分的聚类个数；

（3）聚类簇的形状没有偏倚；

（4）可以在需要时输入过滤噪声的参数。

缺点：

（1）当数据量增大时，要求较大的内存支持I/O消耗也很大；

（2）当空间聚类的密度不均匀、聚类间距差相差很大时，聚类质量较差，因为这种情况下参数MinPts和Eps选取困难

（3）算法聚类效果依赖与距离公式选取，实际应用中常用欧式距离，对于高维数据，存在“维数灾难”。

R语言中的例子：

1
2
3
4
5
6
7
8
#---基于密度的聚类分析
library(fpc)
iris2<-iris[-5]
ds<-dbscan(iris2,eps=0.42,MinPts = 5)
table(ds$cluster,iris$Species)
 
#打印出ds和iris2的聚类散点图
plot(ds,iris2)

6

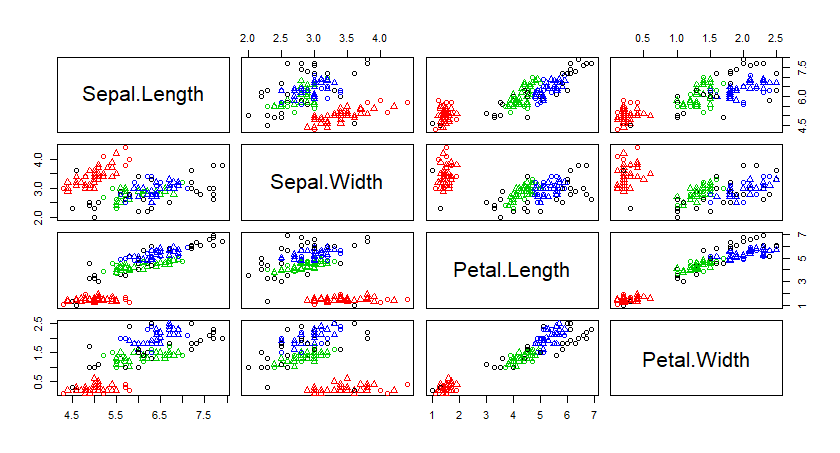
1
2
#打印出iris第一列和第四列为坐标轴的聚类结果
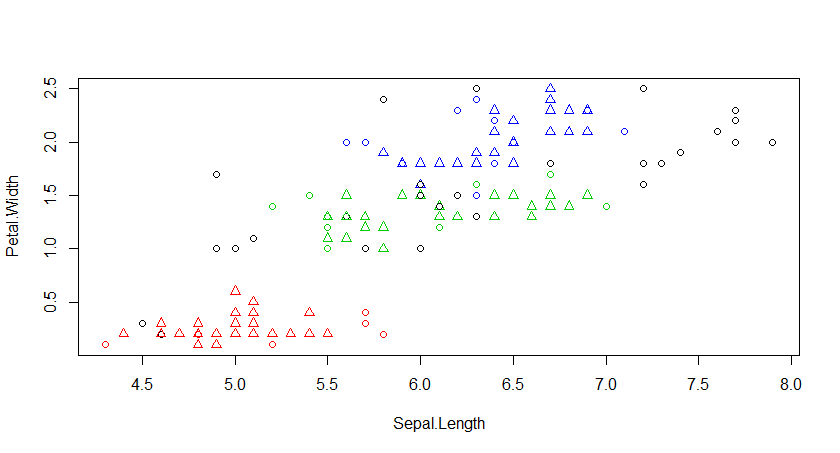
plot(ds,iris2[,c(1,4)])

7

1
2
#另一个表示聚类结果的函数，plotcluster
plotcluster(iris2,ds$cluster)

8

技术工具
#R
【数据挖掘】使用R语言进行聚类分析
https://fulequn.github.io/2020/10/Article202010083/
作者
Fulequn
发布于
2020年10月8日
许可协议