计算机图形学-光栅图形学算法（2）

光栅图形学算法

随着光栅显示器的出现，为了在计算机上处理、显 示图形，需要发展一套与之相适应的算法。

光栅图形算法多数属于计算机图形的底层算法，很多图形学的基本概念和思想都在这一章。

直线段的扫描转换算法

一、直线段的扫描转换算法

在数学上，直线上的点有无穷多个。但当在计算机 光栅显示器屏幕上表示这条直线时需要做一些处理。

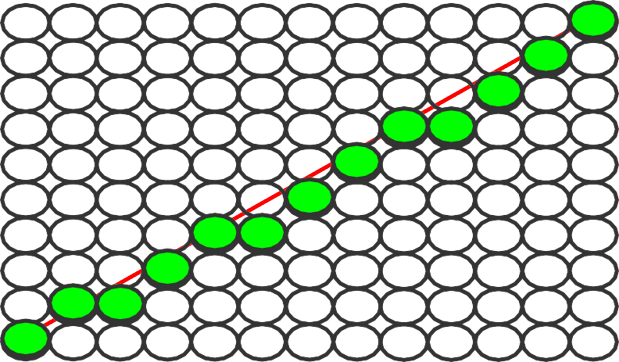
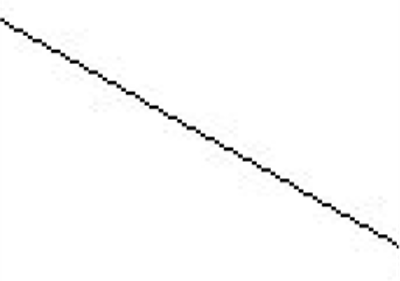
为了在光栅显示器上用这些 离散的像素点逼近这条直 线，需要知道这些像素点的 x，y坐标。

求出过P0,P1(直线的两个端点)的直线段方程：

$$y = kx + b \\ k =(y1-y0)/(x1-x0) \quad (x1≠x0)$$

假设x已知，即从x的起点x0开始，沿x方向前进一个像素（步长= 1)，可以计算出相应的y值。

因为像素的坐标是整数，所以y值还要进行取整处理。

如何把数学上的一个点扫描转换一个屏幕像素点? 取整

直线是最基本的图形，一个动画或真实感图形往往需要调用成千上万次画线程序，因此直线算法的好坏与效率将直接影响图形的质量和显示速度。

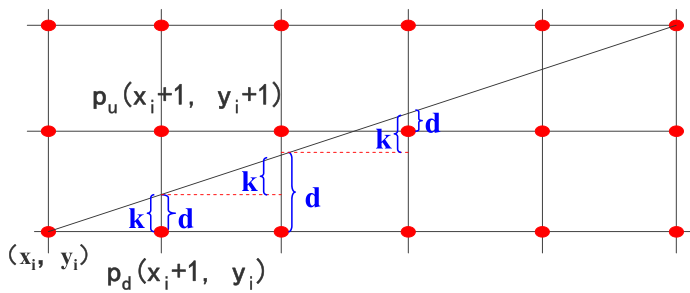
回顾一下刚才的算法：为了提高效率，把计算量减下来，关键问题 就是如何把乘法取消？

二、直线绘制的三个著名的常用算法

1、数值微分法（DDA）

增量思想

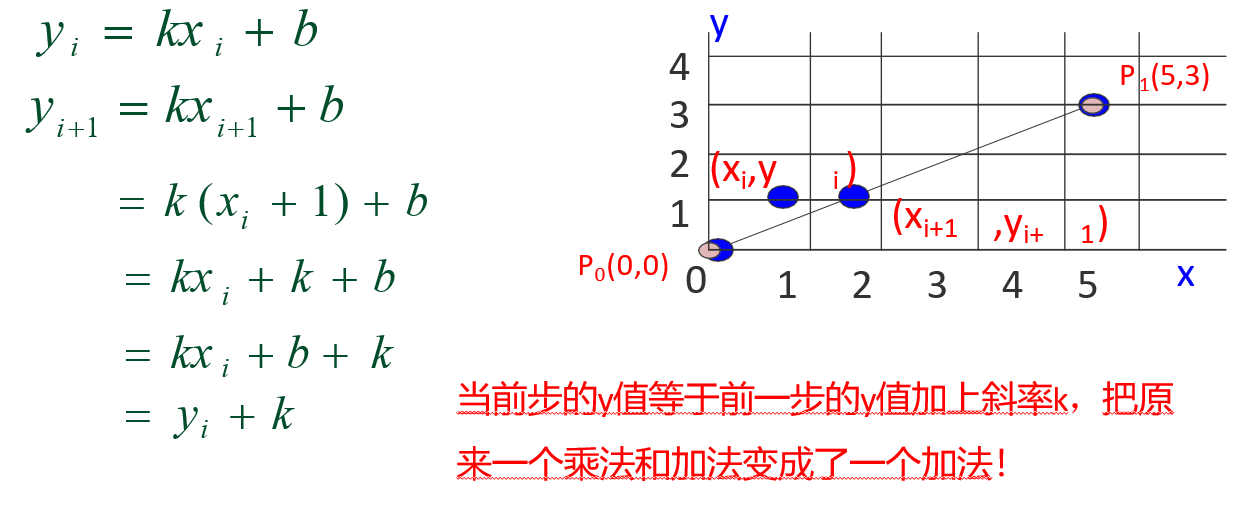
用DDA扫描转换连接两点P0(0,0)和P1(5,3)的直线段。

void DDALine(int x0,int y0,int x1,int y1,int color)     
{
    int x；							
	float dx, dy, y, k;					
	dx, = x1-x0, dy=y1-y0;					   
	k=dy/dx, y=y0;	 					   
	for (x=x0; x<=x1, x++)					   
	{  
		drawpixel (x, int(y+0.5), color);		   
		y=y+k;
    }
}

采用增量思想的DDA算法，直观、易实现，每计算 一个象素坐标，只需计算一个加法。

（1）改进效率。这个算法每步只做一个加法，能否再提高效率？

一般情况下k与y都是小数，而且每一步运算都要对y 进行四舍五入后取整。

唯一改进的途径是把浮点运算变成整数加法!

（2）第二个思路是从直线方程类型做文章

而直线的方程有许多类型，如两点式、一般式等。 如用其它的直线方程来表示这条直线会不会有出人意料的效果？

2、中点画线法

直线的一般式方程：

$$F(x,y)=0 \\ Ax+By+C=0$$

其中A = y0-y1, B = x1-x0, C = x0*y1-x1*y0.

• 对于直线上的点：F ( x , y ) = 0
• 对于直线上方的点：F ( x , y ) > 0
• 对于直线下方的点：F ( x , y ) < 0

基本思想

当前象素点为(xp, yp) 。下一个象素点为P1或P2 。

设M=(xp+1, yp+0.5)，为p1与p2 之中点，Q为理想直线与x=xp+1垂线的交点。将Q与M的y坐标进

行比较。

• M在Q的下方，取P2为下一个象素点；

• M在Q的上方，取P1为下一点。

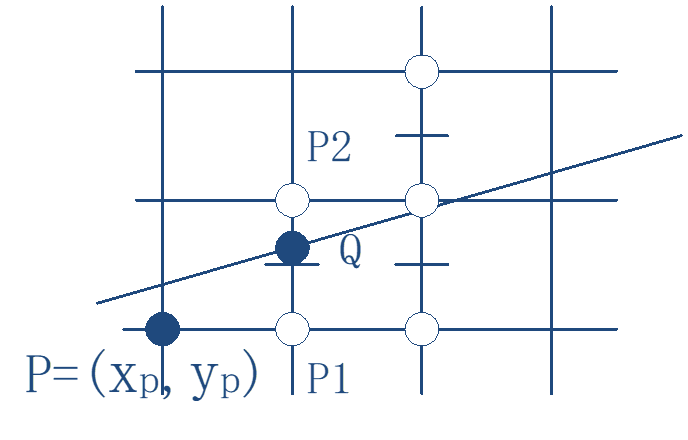
每次在最大位移方向上走一步，而另一个方向是走 步还是不走步要取决于中点误差项的判断。

假定：0≤|k|≤1。因此，每次在x方向上加1，y方向上加1或不变需要判断。

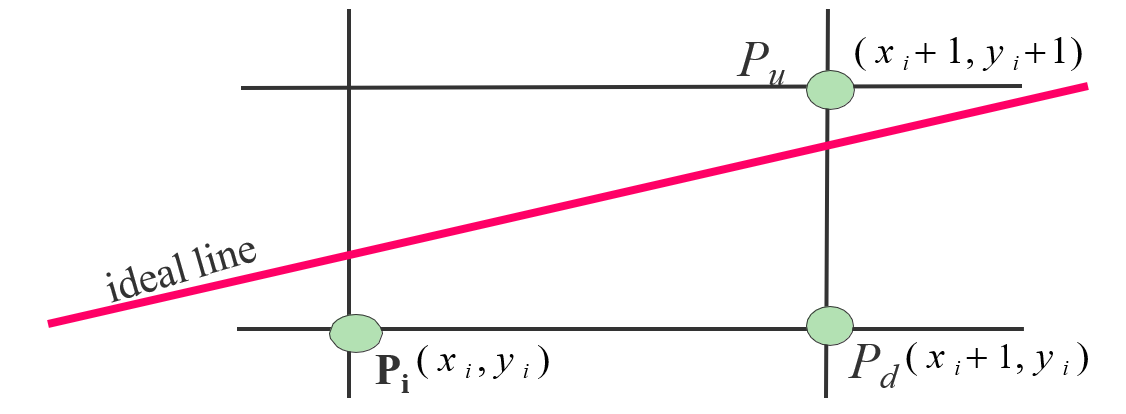
当M在Q的下方，则Pu离直线近，应为下一个象素点。

当M在Q的上方，应取Pd为下一点。

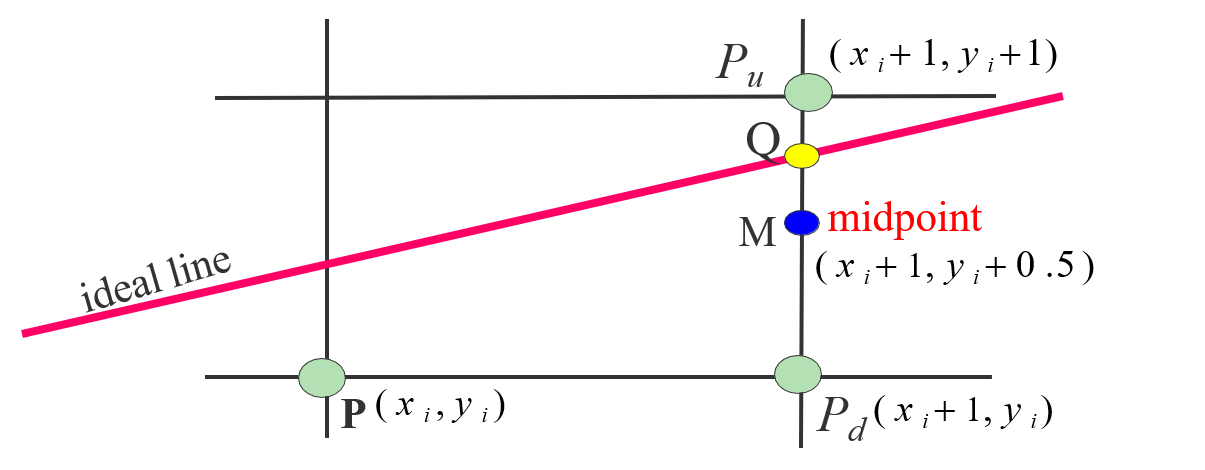
如何判断Q在M的上方还是下方？

把M代入理想直线方程：F ( xm ，ym) = Ax + By + C

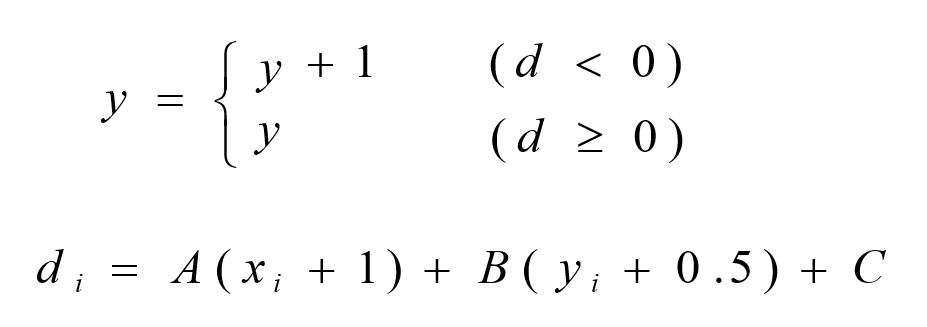
为了求出d值，需要两个乘法，四个加法。

能否也采用增量计算，提高运算效率呢？

d是x,y的线性函数，采用增量计算是可行的。

如何推导出d值的递推公式？

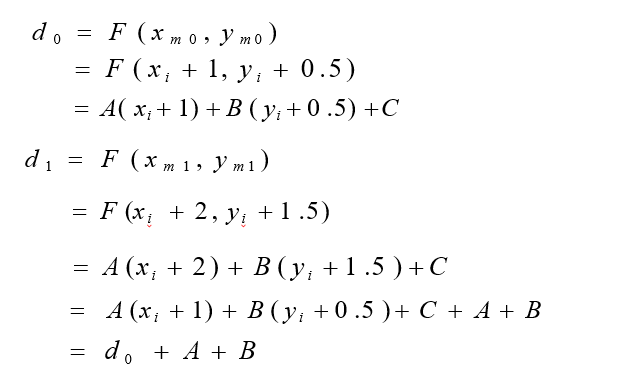
下面计算d的初始值d0，直线的第一个像素P0(x0,y0) 在直线上，因此相应的d的初始值计算如下：

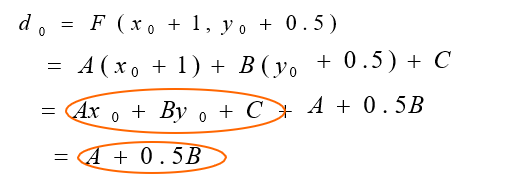
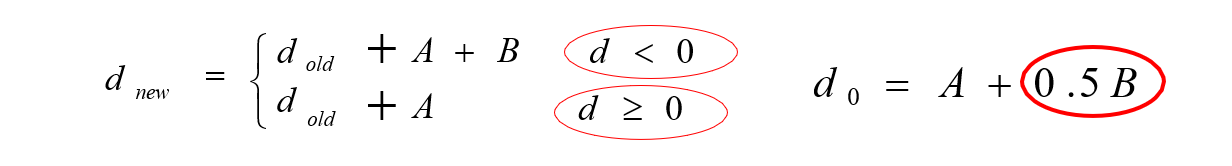
至此，中点算法至少可以和DDA算法一样好！

可以用2d代替d来摆脱浮点运算，写出仅包含整数运的算法。

这样，中点生成直线的算法提高到整数加法，优于DDA算法。

伪代码如下：

void Midpoint Line (int x0,int y0,int x1, int y1,int color)
     {   
          int a, b, d1, d2, d, x, y;
    a=y0-y1, b=x1-x0, d=2*a+b;
    d1=2*a, d2=2* (a+b);
    x=x0, y=y0;
    drawpixel(x, y, color);
    while (x<x1)
    { if (d<0)       {x++, y++, d+=d2; }
     else       {x++, d+=d1;}
     drawpixel (x, y, color);
     }  /* while */
 } /* mid PointLine */

小结

(1) Ax + By + C = 0

(2) 通过判断中点的符号，最终可以只进行整数加法。

这个算法是否还有改进的余地？

能否提出一个算法，使这个算法不但能解决画直线，还能解决圆弧、抛物线甚至自由曲线的光栅化问 题，使算法的覆盖域扩大。

3、Bresenham算法

DDA把算法效率提高到每步只做一个加法。

中点算法进一步把效率提高到每步只做一个整数加法

Bresenham提供了一个更一般的算法。该算法不仅有好的效率，而且有更广泛的适用范围。

该算法的思想是通过各行、各列像素中心构造一组虚拟网格线，按照直线起点到终点的顺序，计算直线与各垂直网格线的交点，然后根据误差项的符号确定该列象素中与此交点最近的象素。

假设每次x+1，y的递增（减）量为0或1，它取决于实际直线与最近光栅网格点的距离，这个距离的最大误差为0.5。

误差项d的初值d0＝0

d＝d＋k

一旦d≥1，就把它减去1，保证d的相对性,且在0、1之间。

圆弧的扫描转换算法

多边形的扫描转换与区域填充算法

裁剪算法

反走样算法

消隐算法